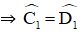Cho 5 điểm A,B,C,D,E chứng minh a/ AB - CD + EA = DB + EC b/ AB + CD + EA = ED - BC

Những câu hỏi liên quan
Cho 6 điểm A, B, C, D, E, F. Chứng minh
a) AB+ CD+ BC+ EA = ED
b) AB+ BC+ CD+ FE+ DF= AE
Giúp mik vs ạ
Chắc là toàn vecto???
a/ \(=\left(\overrightarrow{EA}+\overrightarrow{AB}\right)+\left(\overrightarrow{BC}+\overrightarrow{CD}\right)=\overrightarrow{EB}+\overrightarrow{BD}=\overrightarrow{ED}\)
b/ \(=\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\overrightarrow{CD}+\left(\overrightarrow{DF}+\overrightarrow{FE}\right)\)
\(=\overrightarrow{AC}+\overrightarrow{CD}+\overrightarrow{DE}=\overrightarrow{AD}+\overrightarrow{DE}=\overrightarrow{AE}\)
Đúng 0
Bình luận (0)
4/ Cho tam giác ABC vuông tại B. Kẻ BE vuông góc với AC, Trên tia đối của tia EA lấy điểm D sao cho ED=EA. Biết EC – EA = AB.
a) Chứng minh rằng tam giác ABE = tam giác DBE; AB = BD
b) Kẻ DI là phân giác của góc BDC (I thuộc BC). Chứng minh AB = CD; Tính số đo góc A, góc C
Cho tam giác ABC có góc A=90 độ ,trên cạnh BC lấy điểm D sao cho CD=CA. Tia phân giác của góc C cắt AB tại E
a,Chứng minh tam ACE= tam giác ADE. So sánh độ dài đoạn EA và ED
b, chứng minh góc BED bằng góc DCE. so sánh độ dài EA và ED
c, chứng minh tia phân giác của góc BED vuông góc với EC
Cho tam giác ABC có góc A=90 độ ,trên cạnh BC lấy điểm D sao cho CD=CA. Tia phân giác của góc C cắt AB tại E
a,Chứng minh tam ACE= tam giác ADE. So sánh độ dài đoạn EA và ED
b, chứng minh góc BED bằng góc DCE. so sánh độ dài EA và ED
c, chứng minh tia phân giác của góc BED vuông góc với EC
Cho đường tròn O và hai dây AB, CD bằng nhau và các đường thẳng AB và CD cắt nhau tại điểm E. Biết rằng các điểm B và D nằm trong cùng nửa mặt phẳng bờ AC. Chứng minh:
a) EA=EC và AD=BC.
b) OE vuông góc với AC và DB.
Help me!!!! Thanks mn.
Cho đướng tròn O và hai dây AB, CD bằng nhau và các đường thẳng AB và CD cắt nhau tại E. Biết rằng các điểm B và D nằm trong cùng nửa mặt phẳng bờ AC. Chứng minh:
a) EA=EC và AB=CD
b)OE vuông góc với AC và DB
Cho hình thang cân ABCD (AB//CD), E là giao điểm của hai đường chéo. Chứng minh rằng EA = EB, EC = ED.
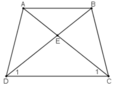
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
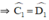
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.
Đúng 1
Bình luận (0)
a) Cho đường tròn (O) có hai dây AB và CD cắt nhau tại điểm E nằm trong đường tròn (O). Chứng minh rằng: EA×EB=EC×ED.
ta có : góc CAB=1/2 sđ cung CB
góc CDB = 1/2 sđ cung CB
-> góc CAB= góc CDB
ta lại có : góc ACD =1/2 sđ cung AD
góc ABD =1/2 sđ cung AD
-> góc ACD = góc ABD
xét tam giác EAC và EDB có;
góc EAC=góc EDB( CMT)
góc ACE= góc DBE(cmt)
-> 2 tam giác đồng dạng theo trường hợp g.g
-> EA/EC=ED/EB
-> EA.EB=EC.ED
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD ( AB//CD), E là giao điểm của 2 đường chéo. Chứng minh rằng EA=EB, EC=ED
Do ABCD là hình thang cân nên AD = BC, AC = BC,
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC chung
Nên ∆ADC = ∆BCD (c.c.c)
Suy ra
Do đó tam giác ECD cân tại E, nên EC = ED
Ta lại có: AC = BD suy ra EA = EB
Chú ý: Ngoài cách chứng minh ∆ADC = ∆BCD (c.c.c) ta còn có thể chứng minh ∆ADC = ∆BCD (c.g.c) như sau:
AD = BC, , DC là cạnh chung.
Đúng 0
Bình luận (0)
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.
Đúng 0
Bình luận (0)
Do ABCD là hình thang cân nên:
AD = BC;
AC = BD;
Xét hai tam giác ADC và BCD, ta có:
AD = BC (gt)
AC = BD (gt)
DC cạnh chung
⇒ ΔADC = ΔBCD (c.c.c)
⇒ ΔECD cân tại E
⇒ EC = ED.
Mà AC = BD
⇒ AC – EC = BD – ED
hay EA = EB.
Vậy EA = EB, EC = ED.
Đúng 0
Bình luận (0)