[ a căn a + b căn b trên căn a + căn b - căn ab ] nhân [căn a + căn b trên a - b]

Những câu hỏi liên quan
Chứng minh đẳng thức
a) căn a/căn a - căn b - căn b/căn a + căn b - 2b/a-b = 1
b) a. căn b + b/ a-b . căn (b^2 -2 .(căn a.b^2 ) +ab/a. (a-2.căn b ) +b . ( căn a + căn b) + b
bài 1rút gọn bt a, 2 căn 10 - 5 trên 4 - căn 10 b, (2/3 căn 3) - (1/4 căn 18) + (2/5 căn 2) - 1/4 căn 12 bài 2:c/m các đẳng thức : [căn x + căn y trên căn x - căn y) - ( căn x - căn y trên căn x + căn y) : căn xy trên x-y =4 bài 3: cho B={[2 căn x trên căn x +3] + [ căn x trên căn x - 3] - 3[ căn x +3] trên x-9} : { [ 2 căn x -2 trên căn x -3] -1} a, rút gọn b, tìm x để P<-1 Mọi ng giúp mk nhé
a căn b-b căn a/căn a-căn b --căn ab
\(=\dfrac{\sqrt{ab}\left(\sqrt{a}-\sqrt{b}\right)}{\sqrt{a}-\sqrt{b}}-\sqrt{ab}=\sqrt{ab}-\sqrt{ab}=0\)
Đúng 1
Bình luận (1)
a) căn 18( căn 2 - căn 3)2
b) a+căn ab / căn a + căn b
c) căn a/b^3 + a/b^4
Cho A= căn x +2 trên căn x -5 và B= 3 trên căn x +5 rồi cộng cho 20-2 căn x trên x-25 đề a)rút gọn B b) tìm x để A=B×|x-4|
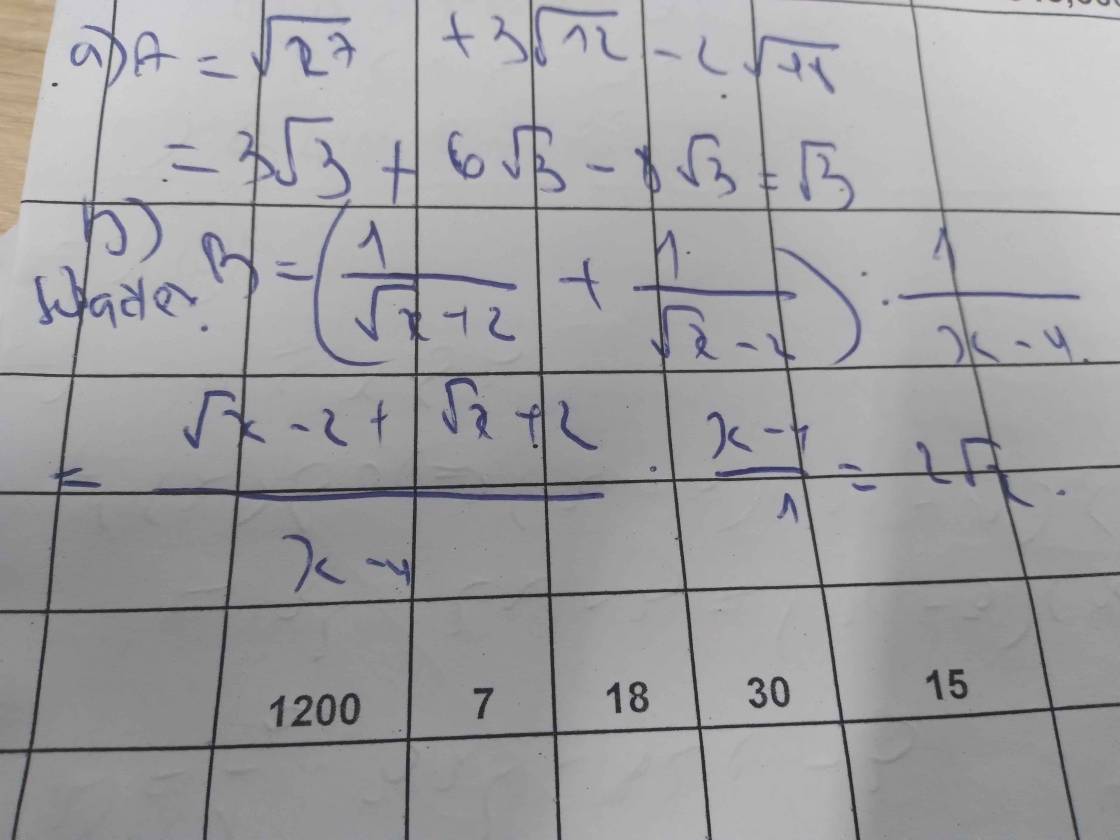
Rút Gọn Bt sau : a, A=căn27 + 3 căn 12 -2 căn 48 b, B= ( 1trên Căn x +2 + 1 trên Căn x-2 ) Chia 1 trên căn x-4 ; Với X lớn hơn 0; x #4
Trục căn ở mẫu:
a) 7 căn 3 - 5 căn 11 trên 3 căn 3 - 7 căn 11
b) 1 trên căn 3 + căn 5 + căn 7
c) 1 trên căn 2 + căn 3 - căn 5
d) 6 trên căn ba của 7 - căn ba của 4
4 trên 1 - căn ba của 5
cho a,b,c>0 và a+b=(căn a+căn b-căn c)^2;căn a+căn b# căn c;b#c Rút gon a+(căn a-căn c)^2/b(căn b-căn c)^2
1/căn a + 1/ căn b =1/căn c CMR : căn (ab)/c - căn bc/a - căn (ca)/b=3
\(\dfrac{1}{\sqrt{a}}+\dfrac{1}{\sqrt{b}}=\dfrac{1}{\sqrt{c}}\Rightarrow\left(\dfrac{1}{\sqrt{a}}+\dfrac{1}{\sqrt{b}}\right)^3=\dfrac{1}{\sqrt{c}^3}\)
\(\dfrac{1}{\sqrt{a}^3}+\dfrac{1}{\sqrt{b}^3}+\dfrac{3}{\sqrt{a}.\sqrt{b}}\left(\dfrac{1}{\sqrt{a}}+\dfrac{1}{\sqrt{b}}\right)-\dfrac{1}{\sqrt{c}^3}=0\)
\(\dfrac{1}{\sqrt{a}^3}+\dfrac{1}{\sqrt{b}^3}+\dfrac{3}{\sqrt{a}.\sqrt{b}.\sqrt{c}}-\dfrac{1}{\sqrt{c}^3}=0\)
\(\dfrac{1}{\sqrt{c}^3}-\dfrac{1}{\sqrt{a}^3}-\dfrac{1}{\sqrt{b}^3}=\dfrac{3}{\sqrt{a}.\sqrt{b}.\sqrt{c}}\)
\(\sqrt{a}.\sqrt{b}.\sqrt{c}\left(\dfrac{1}{\sqrt{c}^3}-\dfrac{1}{\sqrt{b}^3}-\dfrac{1}{\sqrt{a}^3}\right)=3\)
\(\dfrac{\sqrt{ab}}{c}-\dfrac{\sqrt{bc}}{a}-\dfrac{\sqrt{ca}}{b}=3\left(\text{đ}pcm\right)\)
Đúng 0
Bình luận (0)