Giải phương trình
1: 4sin2x + 8cos2x - 9 = 0
2: 1-5sinx + 2cos2x = 0
Những câu hỏi liên quan
Nghiệm của phương trình 1 – 5sinx + 2cos2x 0 là
Đọc tiếp
Nghiệm của phương trình 1 – 5sinx + 2cos2x =0 là
Nghiệm của phương trình
5
-
5
sin
x
+
2
cos
2
x
0
là A. kπ, k ϵ ℤ B. k2π, k ϵ ℤ C.
π
2
+
k
2
π
,
k
∈
ℤ
D.
π
6
+
k
2
π
,
k
∈
ℤ
Đọc tiếp
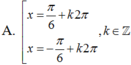
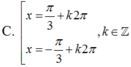
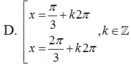
Nghiệm của phương trình 5 - 5 sin x + 2 cos 2 x = 0 là
A. kπ, k ϵ ℤ
B. k2π, k ϵ ℤ
C. π 2 + k 2 π , k ∈ ℤ
D. π 6 + k 2 π , k ∈ ℤ
Giải phương trình sau: 2cos2x - 3√3sin2x - 4sin2x = -4
(k ∈ Z)
B ài tập : Giải các phương trình sau:
a. 2cos2x +5sinx – 4 = 0 ,
b. 2cos2x – 8cosx +5 = 0
c. 2cosx.cos2x = 1+cos2x + cos3x
d. 2(sin44x + cos4x) = 2sin2x – 1
e.sin42x + cos42x = 1 – 2sin4x
f.cos\(\dfrac{4x}{3}\) =cos2x
Xem chi tiết
a. cos2x = 1-sin2x
b. cos2x = 2cos2x - 1
c. 2cosx.cos2x = 1 + cos2x + cos3x
=> 2cosx.cos2x = 2cos2x + 4cos3x - 3cosx
=> cosx(2.(2cos2x - 1) - 2cosx - 4cos2x +3) = 0
=> cosx( -2cosx + 1) = 0
=> cosx=0 hoặc cosx = -1/2
Đúng 0
Bình luận (0)
Giải phương trình sau: 8cos2x + 2sinx – 7 = 0
8cos2x + 2sinx – 7 = 0 (1)
⇔ 8(1 – sin2x) + 2sinx – 7 = 0
⇔ 8sin2x - 2sinx – 1 = 0 (Phương trình bậc hai với ẩn sin x)
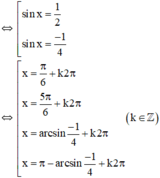
Vậy phương trình có tập nghiệm
{
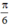+ k2π; 
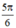+ k2π; arcsin
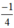+ k2π; π - arcsin
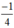+ k2π (k ∈ Z).
Đúng 0
Bình luận (0)
Giải phương trình 3tan2x + 4sin2x - 2
3
tanx - 4sinx + 2 0 A. x ±
π
6
+ k2π, k ∈ Z B. x
π
6
+ kπ, k ∈ Z C. x
-
π
4
+ k2π,
-
π
6
+ k2π, k ∈ Z D. Tất cả sai
Đọc tiếp
Giải phương trình 3tan2x + 4sin2x - 2 3 tanx - 4sinx + 2 = 0
A. x = ± π 6 + k2π, k ∈ Z
B. x = π 6 + kπ, k ∈ Z
C. x = - π 4 + k2π, - π 6 + k2π, k ∈ Z
D. Tất cả sai
Giải phương trình sau: 2cos2x – 3cosx + 1 = 0
2cos2x – 3cosx + 1 = 0 (Phương trình bậc hai với ẩn cos x).
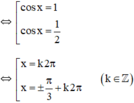
Vậy phương trình có tập nghiệm
Đúng 0
Bình luận (0)
Phương trình
2
cos
2
x
-
3
3
sin
2
x
-
4
sin
2
x
-
4
có họ nghiệm là
Đọc tiếp
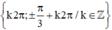
Phương trình 2 cos 2 x - 3 3 sin 2 x - 4 sin 2 x = - 4 có họ nghiệm là
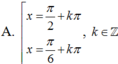
Hướng dẫn giải:
Chọn A.
+ Trường hợp 1.
: là nghiệm của phương trình
+ Trường hợp 2.
: Chia 2 vế phương trình cho cos2x ta được
Đúng 0
Bình luận (0)
Giải phương trình sau: 2cos2x – 3cos x + 1 = 0
2cos2x – 3cosx + 1 = 0 (1)
đặt t = cosx, điều kiện –1 ≤ t ≤ 1
(1) trở thành 2t2 – 3t + 1 = 0
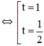(thỏa mãn điều kiện).
+ t = 1 ⇒ cos x = 1 ⇔ x = k.2π (k ∈ Z)
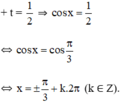
Vậy phương trình có tập nghiệm
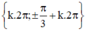(k ∈ Z).
Đúng 0
Bình luận (0)
Giải phương trình
2
cos
2
x
+
π
6
+
4
sin
x
cos
x
-
1
0
Đọc tiếp
Giải phương trình 2 cos 2 x + π 6 + 4 sin x cos x - 1 = 0
