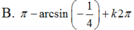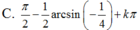2cos2x – 3cosx + 1 = 0 (1)
đặt t = cosx, điều kiện –1 ≤ t ≤ 1
(1) trở thành 2t2 – 3t + 1 = 0
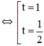 (thỏa mãn điều kiện).
(thỏa mãn điều kiện).
+ t = 1 ⇒ cos x = 1 ⇔ x = k.2π (k ∈ Z)
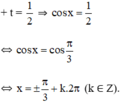
Vậy phương trình có tập nghiệm
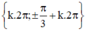 (k ∈ Z).
(k ∈ Z).
2cos2x – 3cosx + 1 = 0 (1)
đặt t = cosx, điều kiện –1 ≤ t ≤ 1
(1) trở thành 2t2 – 3t + 1 = 0
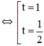 (thỏa mãn điều kiện).
(thỏa mãn điều kiện).
+ t = 1 ⇒ cos x = 1 ⇔ x = k.2π (k ∈ Z)
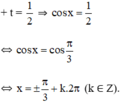
Vậy phương trình có tập nghiệm
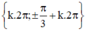 (k ∈ Z).
(k ∈ Z).
Họ nghiệm của phương trình 3cos 4x+ 2cos2x – 5= 0 là
![]()
![]()
![]()
![]()
Giải phương trình sau: 2cos2x – 3cosx + 1 = 0
Giải các phương trình sau: 1 + sin x - cos x - sin 2 x + 2 cos 2 x = 0
Giải phương trình 2 cos 2 x + π 6 + 4 sin x cos x - 1 = 0
![]()
![]()
![]()
![]()
Tìm nghiệm x ∈ 0 ; π 2 của phương trình sau 4 sin 2 π - π 2 - 3 sin π 2 - 2 x = 1 + 2 cos 2 x - π 4
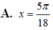
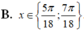
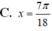
![]()
Giải phương trình sau: 2 cos 2 x - 3 sin 2 x + sin 2 x = 1
Giải phương trình cos x + 3 sin x + 2 cos 2 x + π 3 = 0
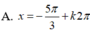
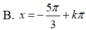
![]()
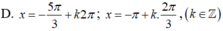
Giải phương trình lượng giác đối với hàm số lượng giác
3cos x - 3=0
Một họ nghiệm của phương trình 2cos2x + 3sin x - 1 = 0 là
![]()