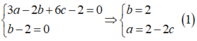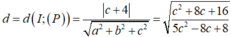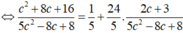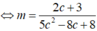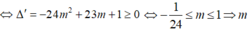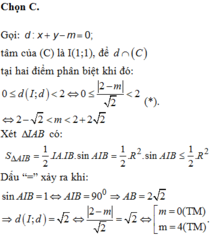3. Cho hai số dương x,y thỏa xy = 3. Tìm giá trị nhỏ nhất của biểu thức P = 3/x + 9/y - 26/3x+y.
(⁄ ⁄•⁄ω⁄•⁄ ⁄) mơn ạ.
4. Cho đường tròn (O), từ điểm A ngoài đường tròn vẽ đường thẳng AO cắt đường tròn (O) tại B,C (AB<AC). Qua A vẽ đường thẳng không đi qua O cắt đường (O) tại D,E (AD<AE). Đường thẳng vuông góc với AB tại A cắt đường thẳng CE tại F.
a) Chứng minh tứ giác ABEF nội tiếp đường tròn.
b) Gọi M là giao điểm thứ của FB với đường tròn (O). Chứng minh DM vuông góc AC.
c) Chứng minh CE.CF + AD.AE = AC².
(๑・ω-)~♥” moahhhh