cho hàm số y = x3 - 6x2 - 1 có 2 điểm cực trị A và B . Điểm nào dưới đây thuộc đường thẳng AB?
A. (1; -9) B. (1; 7) C. ( -1; -7) D. (-1; -9)
Những câu hỏi liên quan
Đồ thị hàm số
y
x
3
-
3
x
2
-
9
x
+
1
có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB? A.
M
0
;
-
1
B.
Q
-
1...
Đọc tiếp
Đồ thị hàm số y = x 3 - 3 x 2 - 9 x + 1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?
A. M 0 ; - 1
B. Q - 1 ; 10
C. P(1;0)
D. N 1 , - 10
TXĐ: D = ℝ .
Ta có:
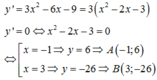
Phương trình đường thẳng đi qua hai điểm A và B là:
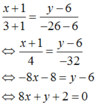
Dựa vào các đáp án ta có . N 1 , - 10 ∈ A B
Chọn D.
Đúng 0
Bình luận (0)
Đồ thị hàm số
y
x
3
-
3
x
2
-
9
x
+
1
có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?
Đọc tiếp
Đồ thị hàm số y = x 3 - 3 x 2 - 9 x + 1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB?
Đồ thị hàm số y = x 3 − 3 x 2 − 9 x + 1 có hai điểm cực trị A và B, Điểm nào dưới đây thuộc đường thẳng AB?
A. M(1;-10)
B. N(-1;10)
C. P(1;0)
D. Q(0;-1)
Đồ thị của hàm số y = x 3 - 3 x 2 - 9 x + 1 có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB ?
A. M(1;-10)
B. M(-1;10)
C. M(1;0)
D. M(0;-1)
Tọa độ các điểm cực trị là A(-1;6) và B(3;-26)
=> đường thẳng đi qua hai điểm cực trị là AB: 8x+2y+2 = 0.
Kiểm tra ta được 
Chọn A.
Đúng 0
Bình luận (0)
Đồ thị hàm số y = x 3 + 3 x 2 - 9 x - 1 có hai cực trị A và B. Điểm nào dưới đây thuộc đường thẳng AB
A. N(0;2)
B. P(-1;1)
C. Q(-1;-8)
D. M(0;-1)
Đồ thị của hàm số
y
x
3
+
3
x
2
−
9
x
+
2
có hai điểm cực trị A ; B Điểm nào dưới đây thuộc đường thẳng AB A.
P
1
;
3
B.
M
0
;
1
C.
Q
3...
Đọc tiếp
Đồ thị của hàm số y = x 3 + 3 x 2 − 9 x + 2 có hai điểm cực trị A ; B Điểm nào dưới đây thuộc đường thẳng AB
A. P 1 ; 3
B. M 0 ; 1
C. Q 3 ; − 29
D. N 0 ; 5
Đáp án D
Ta có y ' = 3 x 2 + 6 x − 9 ; y ' = 0 ⇔ x = 1 x = − 3 . Từ đó 2 điểm cực trị là A 1 ; − 3 ; B − 3 ; 29 . Phương trình đường thẳng A B : y = a x + b , từ đó ta tìm được a = − 8 ; b = 5 . Vậy A B : y = − 8 x + 5 . Có điểm N 0 ; 5 thuộc đường thẳng này.
Đúng 0
Bình luận (0)
Đồ thị hàm số
y
2
x
3
−
6
x
2
−
18
x
có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng ? A.
E
1
;
−
22
.
B.
H
1
;
−...
Đọc tiếp
Đồ thị hàm số y = 2 x 3 − 6 x 2 − 18 x có hai điểm cực trị A và B. Điểm nào dưới đây thuộc đường thẳng ?
A. E 1 ; − 22 .
B. H 1 ; − 10 .
C. K 0 ; 6 .
D. G 3 ; 54 .
Đáp án A
Có y ' = 6 x 2 − 12 x − 18 ; y ' = 0 ⇔ x = − 1 x = 3 . Khi đó 2 điểm cực trị của hàm số là A − 1 ; 10 ; B 3 ; − 54 .Phương trình đường thẳng AB có dạng y = a x + b ; đi qua A và B
⇒ a = − 16 ; b = − 6 . Vậy A B : y = − 16 x − 6 . Đường thẳng này đi E 1 ; − 22 .
Chú ý: Cách khác tìm phương trình AB, ta lấy đa thức 2 x 3 − 6 x 2 − 18 x chia cho y' được dư là − 16 x − 6 thì phương trình A B : y = − 16 x − 6 .
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
6
x
2
+
9
x
-
2
(
C
)
. Đường thẳng đi qua điểm A(-1;1) và vuông góc với đường thẳng đi qua hai điểm cực trị của (C) là: A.
y
-
1
2
x
+
3
2
B.
y
1...
Đọc tiếp
Cho hàm số y = x 3 - 6 x 2 + 9 x - 2 ( C ) . Đường thẳng đi qua điểm A(-1;1) và vuông góc với đường thẳng đi qua hai điểm cực trị của (C) là:
A. y = - 1 2 x + 3 2
B. y = 1 2 x + 3 2
C. y = x + 3
D. x - 2y - 3 = 0
Đáp án B
Ta có y ' = 3 x 2 - 12 x + 9 = 0 ⇔ [ x = 3 ⇒ y = - 2 x = 1 ⇒ y = 2 ⇒ M 3 ; - 2 N 1 ; 2 ⇒ M N : 2 x + y - 4 = 0 .
Phương trình đường thẳng đi qua điểm A(-1;1) và vuông góc với (MN) là (d): y = 1 2 x + 3 2 .
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
−
3
x
−
2
. Trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số nằm trên đường thẳng nào dưới đây? A.
x
+
2
y
+
2
0
B.
2
x
-
y
+
2
0
C.
2
x
+...
Đọc tiếp
Cho hàm số y = x 3 − 3 x − 2 . Trung điểm của đoạn thẳng nối hai điểm cực trị của đồ thị hàm số nằm trên đường thẳng nào dưới đây?
A. x + 2 y + 2 = 0
B. 2 x - y + 2 = 0
C. 2 x + y + 2 = 0
D. 2 x + y - 2 = 0
