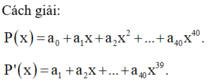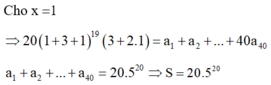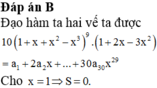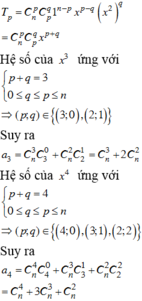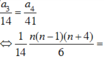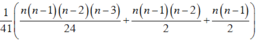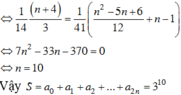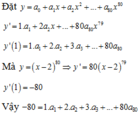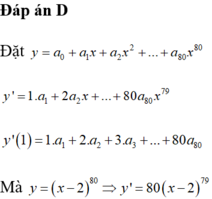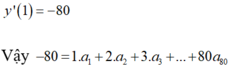Cho khai triển (1+x+x2)20=a0+a1x+a2x2+...+a40x40 tính tổng T=a1+2a2+3a3+...+40a40

Những câu hỏi liên quan
Cho
P
x
1
+
3
x
+
x
2
20
. Khai triển P(x) thành đa thức ta được
P
x
a
0
+
a...
Đọc tiếp
Cho P x = 1 + 3 x + x 2 20 . Khai triển P(x) thành đa thức ta được P x = a 0 + a 1 x + a 2 x 2 + . . . + a 40 x 40 .
Tính S = a 1 + 2 a 2 + . . . + 40 a 40
A. S = - 20 . 5 19
B. S = 20 . 5 21
C. S = 20 . 5 19
D. S = 20 . 5 20
Khai triển
1
+
x
+
x
2
+
x
3
10
a
0
+
a
1
x
+
...
+
a
30
x...
Đọc tiếp
Khai triển 1 + x + x 2 + x 3 10 = a 0 + a 1 x + ... + a 30 x 30 .
Tính tổng S = a 1 + 2 a 2 + ... + 30 a 30 .
A. 5.2 10
B. 0.
C. 4 10 .
D. 2 10 .
Đáp án B
Ta có: 1 + x + x 2 − x 3 10 ' = a 0 + a 1 x + ... + a 30 x 30
' ⇔ 10 1 + x + x 2 − x 3 9 1 + x + x 2 − x 3
a 1 + 2 a 2 x + ... + 30 a 30 x 29 ⇔ 10 1 + x + x 2 − x 3 9 a 1 + 2 a 2 x + ... + 30 a 30 x 29
Chọn: x = 1 ⇒ 10 1 + 1 + 1 − 1 9 .0 = a 1 + 2 a 2 x + ... + 30 a 30
⇔ S = 0
Đúng 0
Bình luận (0)
Khai triển
1
+
x
+
x
2
-
x
3
10
a
0
+
a
1
x
+
.
.
.
+
a
30...
Đọc tiếp
Khai triển 1 + x + x 2 - x 3 10 = a 0 + a 1 x + . . . + a 30 x 30 . Tính tổng S = a 1 + 2 a 2 + . . . + 30 a 30
A. 5 . 2 10
B. 0
C. 4 10
D. 2 10
Khai triển
1
+
x
+
x
2
−
x
3
10
a
0
+
a
1
x
+
...
+
a
30
x...
Đọc tiếp
Khai triển 1 + x + x 2 − x 3 10 = a 0 + a 1 x + ... + a 30 x 30 . Tính tổng S = a 1 + 2 a 2 + ... + 30 a 30
A. 5.2 10
B. 0
C. 4 10
D. 2 10
Đáp án B
Đạo hàm ta hai vế ta được
10 1 + x + x 2 − x 3 9 . 1 + 2 x − 3 x 2 = a 1 + 2 a 2 x + ... + 30 a 30 x 29 Cho x = 1 ⇒ S = 0.
Đúng 0
Bình luận (0)
Cho khai triển
1
-
2
x
n
a
0
+
a
1
x
+
a
2
x...
Đọc tiếp
Cho khai triển 1 - 2 x n = a 0 + a 1 x + a 2 x 2 + . . . + a n x n , biết S = a 1 + 2 a 2 + . . . + n a n = 34992 .Tính giá trị của biểu thức P = a 0 + 3 a 1 + 9 a 2 + . . + 3 n a n
A. -78125.
B. 9765625.
C. -1953125.
D. 390625.
Chọn đáp án D
Ta có
![]()
nên a k = C n k ( - 2 ) k
⇒ a k = 2 k . C n k với 0 ≤ k ≤ n , k ∈ ℕ Suy ra
Xét khai triển
![]()
Đạo hàm hai vế của (*):

Nhân cả hai vế của (**) với x:
![]()
Thay x=2 vào (1) ta được
![]()
⇔ n . 3 n = 52488 = 8 . 3 8 . Suy ra n = 8
Vậy với n = 8 thì P = 390625
Đúng 0
Bình luận (0)
Cho khai triển
1
+
x
+
x
2
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2
n
x...
Đọc tiếp
Cho khai triển 1 + x + x 2 = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n với n ≥ 2 và a 0 , a 1 , a 2 , . . . , a 2 n là các hệ số. Tính tổng S = a 0 + a 1 + a 2 + . . . + a 2 n biết a 3 14 = a 4 41
A. S = 3 10
B. S = 3 12
C. S = 2 10
D. S = 2 12
Cho khai triển
x
-
2
18
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
80
x
80
. Tính tổng
S...
Đọc tiếp
Cho khai triển x - 2 18 = a 0 + a 1 x + a 2 x 2 + . . . + a 80 x 80 . Tính tổng S = 1 . a 1 + 2 . a 2 + 3 . a 3 + . . . + 80 . a 80
A. -70
B. 70
C. -80
D. 80
Cho khai triển
1
+
x
+
x
2
n
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
2...
Đọc tiếp
Cho khai triển 1 + x + x 2 n = a 0 + a 1 x + a 2 x 2 + . . . + a 2 n x 2 n với n ≥ 2 và a 0 , a 1 , a 2 , . . . , a 2 n là các hệ số. Tính tổng S = a 0 + a 1 + a 2 + . . . + a 2 n biết a 3 14 = a 14 41
A. 3 10
B. 3 12
C. 2 10
D. 2 12
Cho khai triển
x
−
2
80
a
0
+
a
1
x
+
a
2
x
2
+
...
+
a
80
x
80
. Tổng
S
1.
a...
Đọc tiếp
Cho khai triển x − 2 80 = a 0 + a 1 x + a 2 x 2 + ... + a 80 x 80 .
Tổng S = 1. a 1 + 2. a 2 + 3. a 3 + ... + 80 a 80 có giá trị là:
A. -70.
B. 80
C. 70
D. -80
Cho khai triển
x
-
2
80
a
0
+
a
1
x
+
a
2
x
2
+
.
.
.
+
a
80...
Đọc tiếp
Cho khai triển x - 2 80 = a 0 + a 1 x + a 2 x 2 + . . . + a 80 x 80 .Tổng S = 1 . a 1 + 2 . a 2 + 3 . a 3 + . . . + 80 a 80 có giá trị là:
A. -70
B. 80
C. 70
D. -80