cho tam giác ABC thỏa mãn : sin2A = sinB . sin C
CMR: cos A >= 1/2
Mong mọi người giúp nhanh
Những câu hỏi liên quan
Cho tam giác ABC. CMR:
a) sinA + sinB + sinC = 4cos(A/2)cos(B/2)cos(C/2)
b) cosA + cosB + cosC = 1 + 4sin(A/2)sin(B/2)sin(C/2)
c) sin2A + sin2B + sin2C = 4sinA.sinB.sinC
d) cos2A + cos2B + cos2C = -(1 + 4cosA.cosB.cosC)
Cho tam giác ABC. CMR:
a) sinA + sinB + sinC = 4cos(A/2)cos(B/2)cos(C/2)
b) cosA + cosB + cosC = 1 + 4sin(A/2)sin(B/2)sin(C/2)
c) sin2A + sin2B + sin2C = 4sinA.sinB.sinC
d) cos2A + cos2B + cos2C = -(1 + 4cosA.cosB.cosC)
Cho tam giác ABC. CMR:
a) sinA + sinB + sinC = 4cos(A/2)cos(B/2)cos(C/2)
b) cosA + cosB + cosC = 1 + 4sin(A/2)sin(B/2)sin(C/2)
c) sin2A + sin2B + sin2C = 4sinA.sinB.sinC
d) cos2A + cos2B + cos2C = -(1 + 4cosA.cosB.cosC)
Cho tam giác ABC. CMR:
a) sinA + sinB + sinC = 4cos(A/2)cos(B/2)cos(C/2)
b) cosA + cosB + cosC = 1 + 4sin(A/2)sin(B/2)sin(C/2)
c) sin2A + sin2B + sin2C = 4sinA.sinB.sinC
d) cos2A + cos2B + cos2C = -(1 + 4cosA.cosB.cosC)
cho tam giác abc. cmr sin^3a*cos(b-c)+sin^3b*cos(c-a)+sin^3c*cos(a-b)=sina*sinb*sinc
cho tam giác abc. cmr sin^3a*cos(b-c0+sin^3b*cos(c-a)+sin^3c*cos(a-b)=sina*sinb*sinc
Cho tam giác ABC thỏa mãn sin2A = sinB. sinC. Hỏi mệnh đề nào đúng.
A. a2 = bc
B. cosA ≥ ½
C. Cả A và B sai
D. Cả A và B đúng
Chọn D.
+ Áp dụng định lí sin ta có
Suy ra sin2A = sinB. Sin C khi và chỉ khi :
Hay a2 = bc
+ Áp dụng định lí côsin và ý trên ta có
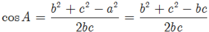
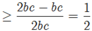
Vậy cả A và B đúng.
Đúng 0
Bình luận (0)
chứng minh tam giác ABC đều
a) sin2A+sin2B+sin2C=sinA+sinB+sinC
b) sin6A + sin6B + sin 6C = 0
c) sin A + sinB + sinC = \(cos\frac{A}{2}+cos\frac{B}{2}+cos\frac{C}{2}\)
d) \(sin\frac{A}{2}.sin\frac{B}{2}.sin\frac{C}{2}=\frac{1}{8}\)
Chứng minh rằng với mọi tam giác ABC ta có:
a) \(SinA+SinB+SinC\le Cos\dfrac{A}{2}+Cos\dfrac{B}{2}+Cos\dfrac{C}{2}\)
b) \(CosA.CosB.CosC\le Sin\dfrac{A}{2}.Sin\dfrac{B}{2}.Sin\dfrac{C}{2}\)