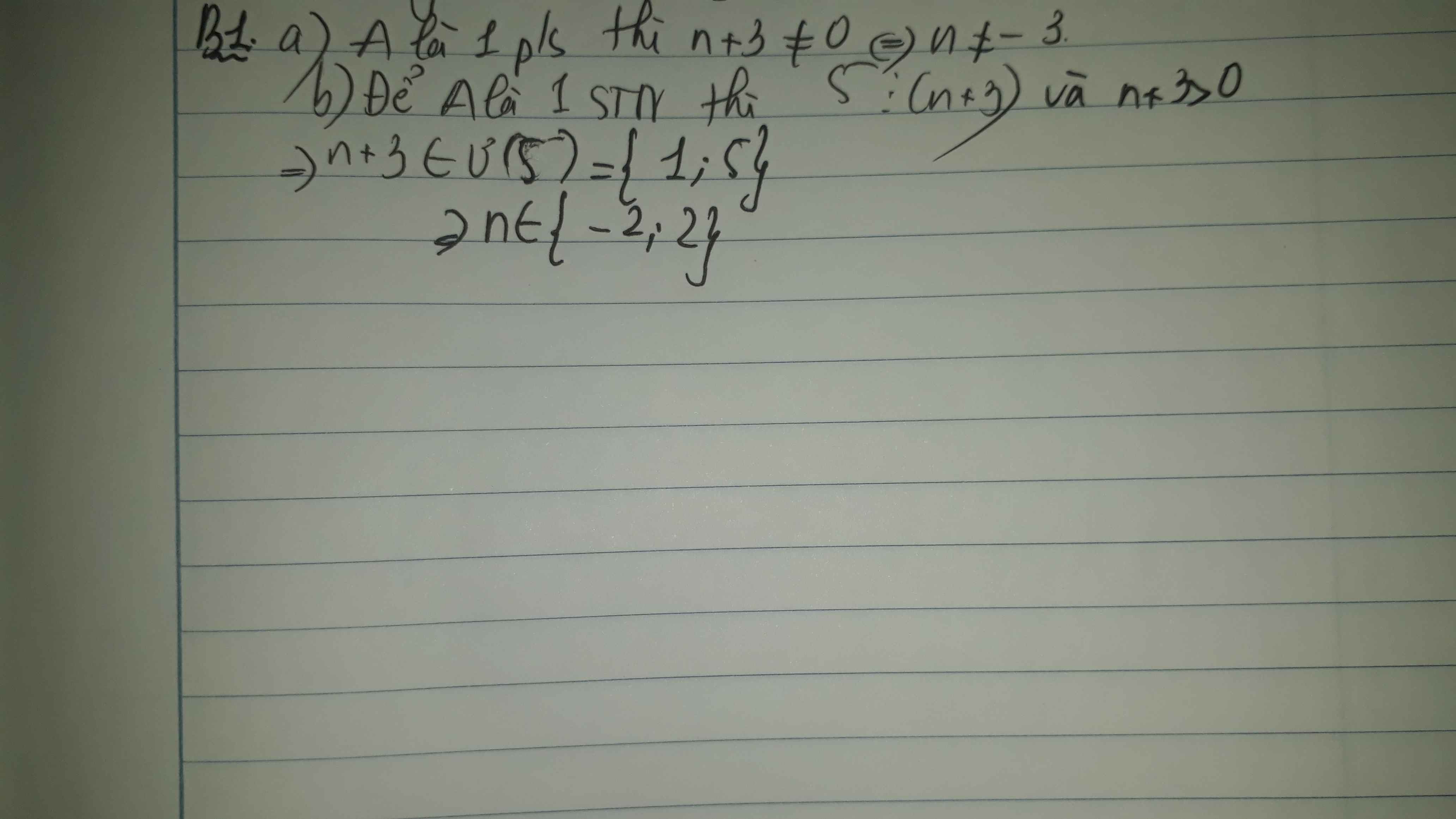Hai bạn Misaki và Ngọc Ánh lập luận sai sai ở đoạn 3n+2 nhé

Bài này mình làm để bạn tham khảo , sai xót bỏ qua nhé 
Ta có \(M=\frac{6n-1}{3n+2}=\frac{6n+4-5}{3n+2}=\frac{2.\left(3n+2\right)-5}{3n+2}=2-\frac{5}{3n+2}\)

Để M có giá trị nhỏ nhất thì \(\frac{5}{3n+2}\)có giá trị lớn nhất

Khi đó 3n +2 có giá trị nhỏ  nhất mà \(n\in Z\)nên 3n + 2 nhỏ nhất khi và chỉ khi \(3n+2=2\)

\(\Rightarrow n=0\)Nên \(M=\frac{6.0-1}{3.0+2}=-\frac{1}{2}\)

Vậy giá trị nhỏ nhất của M = -1/2 khi và chỉ khi n = 0 

Ta có: \(A=\frac{6n-1}{3n+2}=\frac{6n+4-5}{3n+2}=2-\frac{5}{3n-2}.\)

Để A có giá trị nhỏ nhất ( n thuộc N ) thì \(\frac{5}{3n+2}\)đạt giá trị lớn nhất.

=> 3n + 2 đạt giá trị tự nhiên nhỏ nhất

=> 3n đạt giá trị tự nhiên nhỏ nhất

=> n là số tự nhiên nhỏ nhất

=> n = 0

học tốt ~~~

Ta có \(M=\frac{6n-1}{3n+2}=\frac{6n+4-5}{3n+2}=2-\frac{5}{3n+2}\)

Để A đạt giá trị nhỏ nhất (n\(\in N\)) thì \(\frac{5}{3n+2}\)đạt giá trị lớn nhất

=> 3n+2 đạt giá trị tự nhiện nhỏ nhất

=>3n đạt giá trị nhỏ nhất

Mà n\(\in\)N

=> n=0

Vậy n=0 thì\(\frac{6n-1}{3n+2}\)đạt giá trị nhỏ nhất

~Hok tốt~

Bài 2: 

a: Để A là phân số thì \(n+4\ne0\)

hay \(n\ne-4\)

b: Để A là số tự nhiên thì \(3n-5⋮n+4\)

\(\Leftrightarrow-17⋮n+4\)

\(\Leftrightarrow n+4=17\)

hay n=13

M=(6n+4-5):(3n+2)=2-5:(3n+2)

a) để M nguyên thì (3n+2) phải là ước của 5

=> 3n+2={-5; -1; 1; 5}

+/ 3n+2=-5 => n=-7/3 (loại)

+/ 3n+2=-1 => n=-1; M=7

+/ 3n+2=1 => n=-1/3 loại

+/ 3n+2=5 => n=1; M=-3

Đs: n={-1; 1}

b) để M đạt nhỏ nhất thì 5:(3n+2) là lớn nhất, hay 3n+2 đạt giá trị nhỏ nhất => n=0

M​​min=2-5/2=-1/2

a) Để A có giá trị nguyên

suy ra (6n - 1) chia hết cho (3n + 2) 

Vì (3n + 2) chia hết cho (3n + 2) suy ra 2(3n + 2) chia hết cho (3n + 2) hay (6n + 4) chia hết cho (3n + 2)

suy ra [(6n - 1) - (6n + 4)] chia hết cho (3n + 2)

            (6n - 1 - 6n - 4) chia hết cho (3n + 2)

                        5           chia hết cho (3n + 2)

hay 3n + 2 thuộc Ư(5). Mà Ư(5) thuộc {1; -1; 5; -5}

Ta có bảng sau:

                    Vậy n = 1 hoặc n = -1

b) Ta có: A=6n - 1/3n + 2 = 6n + 4 - 5/3n + 2 = 2(3n + 2) - 5/3n + 2 = 2 - 5/3n + 2

Để A min suy ra 5/3n + 2 max

Vì 5 ko thay đổi suy ra 3n + 2 min và 5/3n + 2 là số âm nhỏ nhất

Suy ra 3n + 2 là số âm lớn nhất nên 3n + 2 = -1

                                                              3n   = -1 - 2 = -3

                                                                n   = -3 : 3 = -1

                                  Vậy min A = -7 tại n = -1 

Nhớ k mình đúng nhé!!!Thanks các bạn nhiều

Ta có: \(A=\frac{6n-1}{3n+2}=\frac{6n+4-5}{3n+2}=2-\frac{5}{3n+2}\). Để A có giá trị nhỏ nhất (n thuộc N) thì \(\frac{5}{3n+2}\) đạt giá trị lớn nhất.

-> 3n+2 đạt giá trị tự nhiên nhỏ nhất

-> 3n đạt giá trị tự nhiên nhỏ nhất

-> n là số tự nhiên nhỏ nhất

-> n = 0

theo mình thì đúng rùi

nhưng nếu n =0 thì giá trị của M sẽ là -0,5. Mình nghĩ n = 1 thì giá trị của M sẽ la 1.Bạn nào thấy đúng thì k cho mink nha