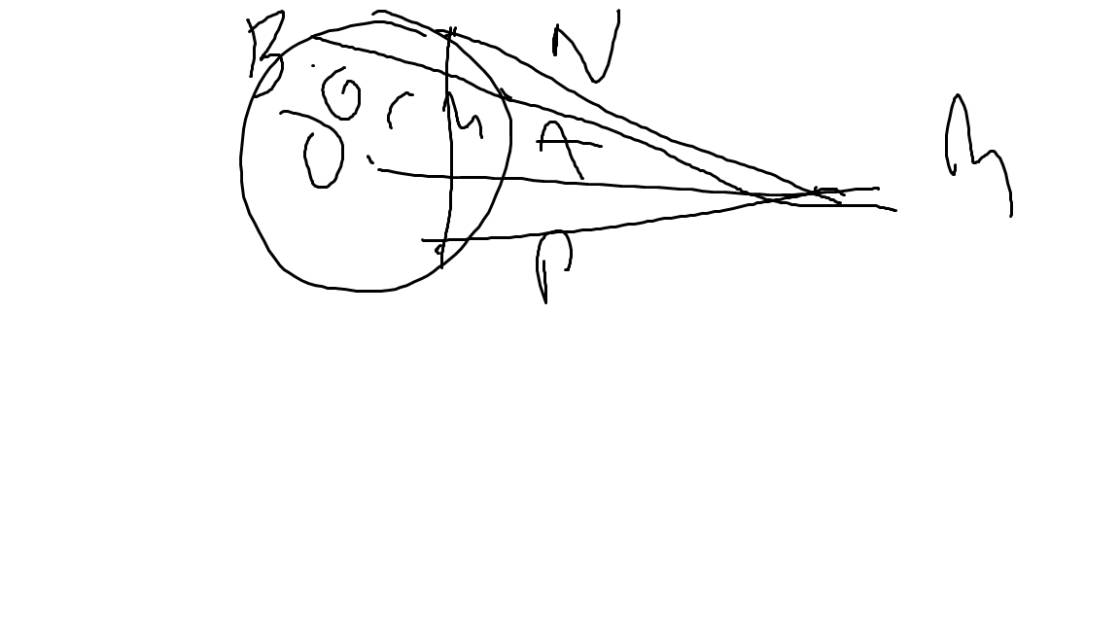
bài tập: Từ một điểm A ở bên ngoài đường tròn (O;R), vẽ hai tiếp tuyến AB, AC (B, C là hai tiếp điểm), và cát tuyến AMN. Gọi I là trung điểm của dây MN.
a) Chứng minh 5 điểm A, B, I, O, C cùng nằm trên một đường tròn.
b) Nếu AB = OB thì tứ giác ABOC là hình gì? Vì sao?
c) Cho AB = R. Tính diện tích hình tròn và độ dài đường tròn ngoại tiếp tứ giác ABOC theo R
ai biết chỉ giúp mình với mình đang cần gaaaaapsppppp lắm.

Những câu hỏi liên quan
Bài 9 . Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là 2 tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E).
a) Chứng minh bốn điểm A, B, O, C cùng thuộc một đường tròn.
b) Gọi H là giao điểm của AO với BC. Chứng minh: OAvuông góc BC và
OD2 = OH.OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA.
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD(=R)
nên \(OH\cdot OA=OD^2\)
=>\(\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
Xét ΔOHD và ΔODA có
\(\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
\(\widehat{HOD}\) chung
Do đó: ΔOHD đồng dạng với ΔODA
Đúng 1
Bình luận (0)
Từ một điểm a ở bên ngoài đường tròn tâm O,kẻ hai tiếp tuyến AB,AC với đường tròn này
Bài 27 (trang 115 SGK Toán 9 Tập 1)
Từ một điểm $A$ nằm bên ngoài đường tròn $(O)$, kẻ các tiếp tuyến $AB$, $AC$ với đường tròn ($B$, $C$ là các tiếp điểm). Qua điểm $M$ thuộc cung nhỏ $BC$, kẻ tiếp tuyến với đường tròn $(O)$, nó cắt các tiếp tuyến $AB$ và $AC$ theo thứ tự ở $D$ và $E$. Chứng minh rằng chu vi tam giác $ADE$ bằng $2AB$.
Ta có
DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)
\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)
\(=AB+AC=2AB\)
Theo tính chất hai tiếp tuyến cắt nhau ta có: .
Chu vi tam giác bằng :
.
Theo tính chất hai tiếp tuyến cắt nhau ta có: .
Chu vi tam giác bằng :
.
Xem thêm câu trả lời
Từ điểm A ở bên ngoài đường tròn (O), kẻ 2 tiếp tuyến AB và AC đến đường tròn (O) (B, C là tiếp điểm). Kẻ cát tuyến ADE vs đường tròn (O) (D nằm giữa A và E).
a) Cm: 4 điểm A, B, O, C cùng thuộc một đường tròn
b) Cm OA ⊥ BC tại H và OD² = OH × OA. Từ đó suy ra tam giác OHD đồng dạng vs tam giác ODA.
Giải và vẽ hình giúp mình vớiii !! :(
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,C,O cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD
nên \(OD^2=OH\cdot OA\)
=>\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
Xét ΔODA và ΔOHD có
\(\dfrac{OD}{OH}=\dfrac{OA}{OD}\)
\(\widehat{DOA}\) chung
Do đó: ΔODA đồng dạng với ΔOHD
Đúng 1
Bình luận (0)
Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là 2 tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E). a) Chứng minh: bốn điểm A, B, O, C cùng thuộc một đường tròn. b) Chứng minh: OA BC tại H và OD2 OH.OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA. c) Chứng minh BC trùng với tia phân giác của góc DHE. d) Từ D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, BC lần lượt tại M và N. Chứng minh: D là trung điểm của MN
Đọc tiếp
Từ điểm A ở bên ngoài đường tròn (O), kẻ hai tiếp tuyến AB, AC đến đường tròn (O) (B, C là 2 tiếp điểm). Kẻ cát tuyến ADE với đường tròn (O) (D nằm giữa A và E). a) Chứng minh: bốn điểm A, B, O, C cùng thuộc một đường tròn. b) Chứng minh: OA BC tại H và OD2 = OH.OA. Từ đó suy ra tam giác OHD đồng dạng với tam giác ODA. c) Chứng minh BC trùng với tia phân giác của góc DHE. d) Từ D kẻ đường thẳng song song với BE, đường thẳng này cắt AB, BC lần lượt tại M và N. Chứng minh: D là trung điểm của MN
a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H
Xét ΔOBA vuông tại B có BH là đường cao
nên \(OH\cdot OA=OB^2\)
mà OB=OD(=R)
nên \(OH\cdot OA=OD^2\)
=>\(\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
Xét ΔOHD và ΔODA có
\(\dfrac{OH}{OD}=\dfrac{OD}{OA}\)
\(\widehat{HOD}\) chung
Do đó: ΔOHD đồng dạng với ΔODA
Đúng 0
Bình luận (0)
Cho đường tròn tâm (O) cố định . Từ một điểm A cố định ở bên ngoài đường tròn (O) kẻ các tiếp tuyến AM và An với đường tròn ( M và N là các tiếp điểm ) đường thẳng qua A cắt đường tròn tâm (O) tại hai điểm B và C ( B nằm giữa A và C ) gọi I là trung điểm BC . a, chứng minh tứ giác amon nội tiếp. b, gọi k là giao điểm của MN và BC . chứng minh tam giác AKM đồng dạng tam giác AMI và AK.AIAB.AC
Đọc tiếp
Cho đường tròn tâm (O) cố định . Từ một điểm A cố định ở bên ngoài đường tròn (O) kẻ các tiếp tuyến AM và An với đường tròn ( M và N là các tiếp điểm ) đường thẳng qua A cắt đường tròn tâm (O) tại hai điểm B và C ( B nằm giữa A và C ) gọi I là trung điểm BC . a, chứng minh tứ giác amon nội tiếp.
b, gọi k là giao điểm của MN và BC . chứng minh tam giác AKM đồng dạng tam giác AMI và AK.AI=AB.AC
Cho đường tròn tâm (O) cố định . Từ một điểm A cố định ở bên ngoài đường tròn (O) kẻ các tiếp tuyến AM và An với đường tròn ( M và N là các tiếp điểm ) đường thẳng qua A cắt đường tròn tâm (O) tại hai điểm B và C ( B nằm giữa A và C ) gọi I là trung điểm BC . a, chứng minh tứ giác amon nội tiếp.
b, gọi k là giao điểm của MN và BC . chứng minh tam giác AKM đồng dạng tam giác AMI và AK.AIAB.AC
Đọc tiếp
Cho đường tròn tâm (O) cố định . Từ một điểm A cố định ở bên ngoài đường tròn (O) kẻ các tiếp tuyến AM và An với đường tròn ( M và N là các tiếp điểm ) đường thẳng qua A cắt đường tròn tâm (O) tại hai điểm B và C ( B nằm giữa A và C ) gọi I là trung điểm BC . a, chứng minh tứ giác amon nội tiếp. b, gọi k là giao điểm của MN và BC . chứng minh tam giác AKM đồng dạng tam giác AMI và AK.AI=AB.AC
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔAKM và ΔAMI có
góc AMK=góc AIM
góc MAK chung
=>ΔAKM đồng dạng với ΔAMI
=>AK/AM=AM/AI
=>AM^2=AI*AK
Xét ΔABM và ΔAMC có
góc AMB=góc ACM
góc BAM chung
=>ΔABM đồng dạng với ΔAMC
=>AB/AM=AM/AC
=>AM^2=AB*AC=AK*AI
Đúng 0
Bình luận (0)
Từ một điểm T ở bên ngoài đường tròn (O), vẽ hai tiếp tuyếnTA; TB với đường tròn (O) (A; B là tiếp điểm). Tia TO cắt đường tròn (O) tại hai điểm phân biệt C và D (C nằm giữa T và O) và cắt đoạn thẳng AB tại điểm F.1) Cho ∠ADB 550. Tính ∠TAB; AOB2) Chứng minh: Tứ giác TAOB nội tiếp3) Chứng minh TC.TD TF.TO4) Chứng minh C là tâm đường tròn nội tiếp DTAB5*) Vẽ đường kính AG của đường tròn (O). Gọi H là chân đường vuông góc kẻ từ điểm B đến AG, I là giao điểm của TG và BH. Chứng minh I là trung đ...
Đọc tiếp
Từ một điểm T ở bên ngoài đường tròn (O), vẽ hai tiếp tuyếnTA; TB với đường tròn (O) (A; B là tiếp điểm). Tia TO cắt đường tròn (O) tại hai điểm phân biệt C và D (C nằm giữa T và O) và cắt đoạn thẳng AB tại điểm F.
1) Cho ∠ADB = 550. Tính ∠TAB; AOB
2) Chứng minh: Tứ giác TAOB nội tiếp
3) Chứng minh TC.TD = TF.TO
4) Chứng minh C là tâm đường tròn nội tiếp DTAB
5*) Vẽ đường kính AG của đường tròn (O). Gọi H là chân đường vuông góc kẻ từ điểm B đến AG, I là giao điểm của TG và BH. Chứng minh I là trung điểm của BH
1: góc ADB=55 độ
góc ADB=góc TAB(=1/2sđ cung AB)
=>góc TAB=55 độ
góc AOB=2*55=110 độ
2:
góc TAO+góc TBO=180 độ
=>TAOB nội tiếp
3: Xét ΔTAC và ΔTDA có
góc TAC=góc TDA
góc ATC chung
=>ΔTAC đồng dạng với ΔTDA
=>TA/TD=TC/TA
=>TA^2=TD*TC
Xét (O) có
TA,TB là tiếp tuyến
=>TA=TB
mà OA=OB
nên OT là trung trực của AB
=>OT vuông góc AB tại F
ΔOAT vuông tại A có AF là đường cao
nên TF*TO=TA^2
=>TF*TO=TC*TD
Đúng 0
Bình luận (0)
Từ một điểm M ở bên ngoài đường tròn (O;6cm) kẻ hai tiếp tuyến MN, MP với đường tròn (N;P€(O)) và cát tuyến MAB của (O) sao cho AB=6cm