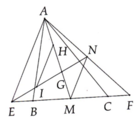
Cho tam giác ABC đường trung tuyến AM và trọng tâm G. Trên tia đối của tia MA lấy các điểm I và K sao cho MI = MG, IK = IG. Gọi N là trung điểm của CK. Chứng minh rằng ba điểm B, I, N thẳng hàng.

Những câu hỏi liên quan
Tam giác ABC có đường trung tuyến AM,trọng tâm G, trên tia đối của tia MA lấy 2 điểm I và K sao cho M là trung điểm của IG .Y là trung điểm KG.gọi N là trung điểm CK
A)Chứng minh I là trọng tâm của tam giác KBCb) Ba điểm BIN thẳng hàng
T
Tam giác ABC có đường trung tuyến AM, trọng tâm G, trên tia đối của tia MA lấy 2 điểm I và K sao cho M là trung điểm của IG , I là trung điểm của KG,Gọi N là TĐ của CK
a) chứng minh I là trọng tâm của tam giác KBC
b)3 điểm BIN thẳng hàng
Toán lớp 7 anh em giúp mình chứng minh mai mình phải nộp bài rùi à ~ Giúp nhé
Bài 1:Cho tam giác ABC, trung tuyến AM, trọng tâm G. I, K thuộc tia đối AM sao cho MIMG, IKIG. N là tủng điểm của CK.Chứng minh: B, I, N thẳng hàng.Bài 2: G là trọng tâm của tam giác ABC, G thuộc AG sao cho G là trung điểm của AG.a) So sánh các cạnh của tam giác BGG với các đường trung tuyến của tam giác ABC.b) So sánh các đường trung tuyến của tam giac BGG với các cạnh của tam giac ABC.Giải chi tiết nhá m.n. Tks m.n trước :)
Đọc tiếp
Bài 1:Cho tam giác ABC, trung tuyến AM, trọng tâm G. I, K thuộc tia đối AM sao cho MI=MG, IK=IG. N là tủng điểm của CK.
Chứng minh: B, I, N thẳng hàng.
Bài 2: G là trọng tâm của tam giác ABC, G' thuộc AG sao cho G là trung điểm của AG'.
a) So sánh các cạnh của tam giác BGG' với các đường trung tuyến của tam giác ABC.
b) So sánh các đường trung tuyến của tam giac BGG' với các cạnh của tam giac ABC.
Giải chi tiết nhá m.n. Tks m.n trước :)
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE CF.a) Chứng minh G là trọng tâm tam giác AEF.b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH MN.
Đọc tiếp
Cho tam giác ABC, trung tuyến AM và trọng tâm G. Trên tia đối của tia BC lấy điểm E, trên tia đối của tia CB lấy điểm F sao cho BE = CF.
a) Chứng minh G là trọng tâm tam giác AEF.
b) Gọi N là trung điểm của AF. Chứng minh ba điểm E, G, N thẳng hàng.
c) Gọi H là trung điểm của GA, I là trung điểm GE. Chứng minh IH // MN và IH = MN.
1. Cho tam giác ABC, trung tuyến AM, trọng tâm G. I và K thuộc tia đối MA sao cho MI = MG, IK = IG. N là trung điểm của CK. Chứng minh B, I ,N thẳng hàng
GIÚP MỚI! MAI NỘP RỒI!
Cho tam giác ABC, trung tuyến AM, trọng tâm G. I, K thuộc tia đối MA sao cho MI=MG, IK=IG. N là trung điểm của CK.
Chứng minh: B, I, N thẳng hàng.
Giải chi tiết nhá m.n. Tks nhiều :)
Cho tam giácABC có các trung tuyến AM, BN gặp nhau tại G. Trên tia đối của tia MA lấy điểm K sao cho MK=MG.
a) CM:GK= AG.
b) CM: tam giác BMK= tam giác CMG.
c)Trên tia đối của tia MA lấy điểm Q sao cho MQ= AM và trên tia đối của tia NB lấy điểm I sao cho NI= BN. Chứng minh rằng ba điểm Q,C,I thẳng hàng.
Tam giác ABC có: G là giao điểm của trung tuyến AM và BN (gt)
=> G là trọng tâm tam giác ABC
=>GM = 1/2 GA (đ/lí 3 trung tuyến của tam giác) (1)
Có GM = MK (gt)
Mà GM + MK = GK
=> GM = MK = 1/2 GK (2)
Từ (1)(2) => GA = GK
b, Xét tam giác BMK và tam giác CMG
BM = CM (gt)
góc BMK = góc CMG (đối đỉnh)
MK = MG (gt)
=> tam giác BMK = tam giác CMG (c.g.c)
c, Xét tam giác ABM và tam giác QCM
MA = QM (gt)
góc AMB = góc QMC ( đối đỉnh)
MB = MC (gt)
=> tam giác ABM = tam giác QCM(c.g.c)
=> góc BAQ = góc CQA ( cặp góc tương ứng)
=> AB // QC ( vì góc BAQ và góc CQA là 2 góc so le trong (3)
Xét tam giác BAN và tam giác ICN
BN = NI (gt)
góc BNA = góc INC (đối đỉnh)
AN = CN (gt)
=> tam giác BAN = tam giác ICN (c.g.c)
=> góc BAN = góc ICN (cặp góc tương ứng)
=> AB // CI (vì góc BAN và góc ICN là 2 góc so le trong) (4)
Từ (3)(4) => Q, C, I thẳng hàng
Đúng 0
Bình luận (0)
Cho ∆ABC nhọn có các đường trung tuyến AM và CN cắt nhau tại G, Trên tia đối của tia MA lấy điểm E sao cho ME = MG. Chứng minh rằng :
a, ∆BMG = ∆CME
b, BG // EC
c, Gọi I trung điểm của BE, AI cắt BG tại F. Chứng minh : 3 điểm E,F,N thẳng hàng.
a: Xet ΔBMG và ΔCME có
MB=MC
góc BMG=góc CME
MG=ME
=>ΔBMG=ΔCME
b: Xet tứ giác BGCE co
M là trung điểm chung của BC và GE
=>BGCE là hình bình hành
=>BG//CE
c: Xét ΔABE co
AI,BG là trung tuyến
AI cắt BG tại F
=>F là trọng tâm
=>E,F,N thẳng hàng
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\)có AM là đường trung tuyến, G là trọng tâm. Trên tia đối của tia GB lấy điểm K sao cho GK=GB. Gọi N là trung điểm của KC, BN cắt CG tại I. Chứng minh ba điểm K,I,M thẳng hàng.