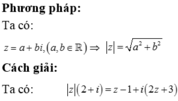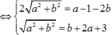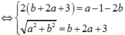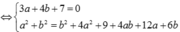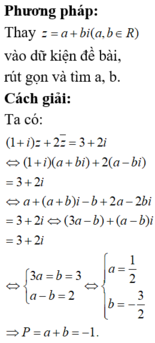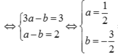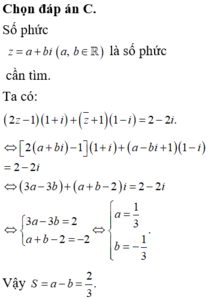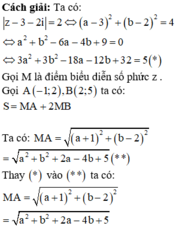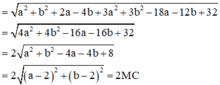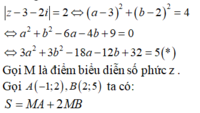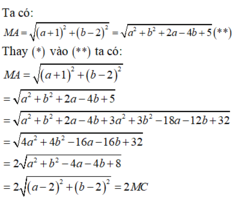cho z=a+bi thỏa \(|z|\)(2+i)=z-1+i(2z+3). tính S=a+b
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6

Những câu hỏi liên quan
Cho số phức thỏa mãn: za+bi,
(
a
,
b
∈
R
)
thỏa mãn:
z
(
2
+
i
)
z
-
1
+
i
(
2
z
+
3
)
. Tính S a + b
Đọc tiếp
Cho số phức thỏa mãn: z=a+bi, ( a , b ∈ R ) thỏa mãn: z ( 2 + i ) = z - 1 + i ( 2 z + 3 ) . Tính S = a + b
![]()
![]()
![]()
![]()
Cho số phức
z
a
+
b
i
(
a
,
b
∈
R
)
thỏa mãn
(
1
+
i
)
z
+
2
z
¯
3
+
2
i
. Tính
P
a
+
b
Đọc tiếp
Cho số phức z = a + b i ( a , b ∈ R ) thỏa mãn ( 1 + i ) z + 2 z ¯ = 3 + 2 i . Tính P = a + b
![]()
![]()
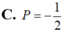
Cho số phức za+bi
a
,
b
∈
R
thỏa mãn
(
1
+
i
)
z
+
2
z
¯
3
+
2
i
. Tính Pa+b
Đọc tiếp
Cho số phức z=a+bi a , b ∈ R thỏa mãn ( 1 + i ) z + 2 z ¯ = 3 + 2 i . Tính P=a+b
![]()
![]()
![]()
![]()
Cho số phức
z
a
+
b
i
(
a
,
b
∈
R
)
thỏa mãn
2
z
-
1
1
+
i
+
z
¯
+
1
1...
Đọc tiếp
Cho số phức z = a + b i ( a , b ∈ R ) thỏa mãn 2 z - 1 1 + i + z ¯ + 1 1 - i = 2 - 2 i Giá trị S=a-b bằng bao nhiêu?
A. S=0
B. S=1
C. S = 2 3
D. S = 1 3
Xét các số phức
z
a
+
b
i
thỏa mãn
z
-
3
-
2
i
2
. Tính a-b biết biểu thức
S
z
+
1
-
2
i
+
2
z...
Đọc tiếp
Xét các số phức z = a + b i thỏa mãn z - 3 - 2 i = 2 . Tính a-b biết biểu thức S = z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
A. - 3
B. 3
C. 4
D. 0
Xét các số phức z a +bi thỏa mãn
z
-
3
-
2
i
2
Tính a-b biết biểu thức
S
z
+
1
-
2
i...
Đọc tiếp
Xét các số phức z = a +bi thỏa mãn z - 3 - 2 i = 2 Tính a-b biết biểu thức S = z + 1 - 2 i + 2 z - 2 - 5 i đạt giá trị nhỏ nhất.
A. - 3
B. 3
C. 4
D. 0
Cho số phức
z
a
+
b
i
thỏa mãn
z
-
i
2
v
à
z
+
3
i
+
2
z
-
4
-
i
đạt giá trị nhỏ nhất. Tổng...
Đọc tiếp
Cho số phức z = a + b i thỏa mãn z - i = 2 v à z + 3 i + 2 z - 4 - i đạt giá trị nhỏ nhất. Tổng a + b bằng
A. 3 + 6 13 17
B. 1 + 2 13 17
C. 5 + 10 13 17
D. 5 - 10 13 17
Chọn C
Cách giải:

=>M thuộc đường tròn (C) tâm I(0,1), R=2

Mà M nằm trên (C) => M là giao điểm của (C) và OB

Đúng 0
Bình luận (0)
Câu 1 : Cho số phức z thỏa mãn z + ( 2 - i )overline{z} 3 - 5i. Môđun của số phức w z - i bằng bao nhiêu ?Câu 2 : Cho số phức z a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )z + ( 2 - i )2 4 + i. Tính P a - b
Đọc tiếp
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z = a + bi, (a, b ∈ ℝ ) thỏa mãn z + 1 + 3i - |z|i = 0. Tính S = a + 3b
A. S = 7 3
B. S = -5
C. S = 5
D. S = - 7 3
Đáp án B
Ta có:
![]()
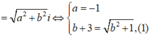
Với b
⩾
-3 thì (1) tương đương với: 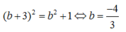
Vậy a + 3b = -5
Đúng 0
Bình luận (0)