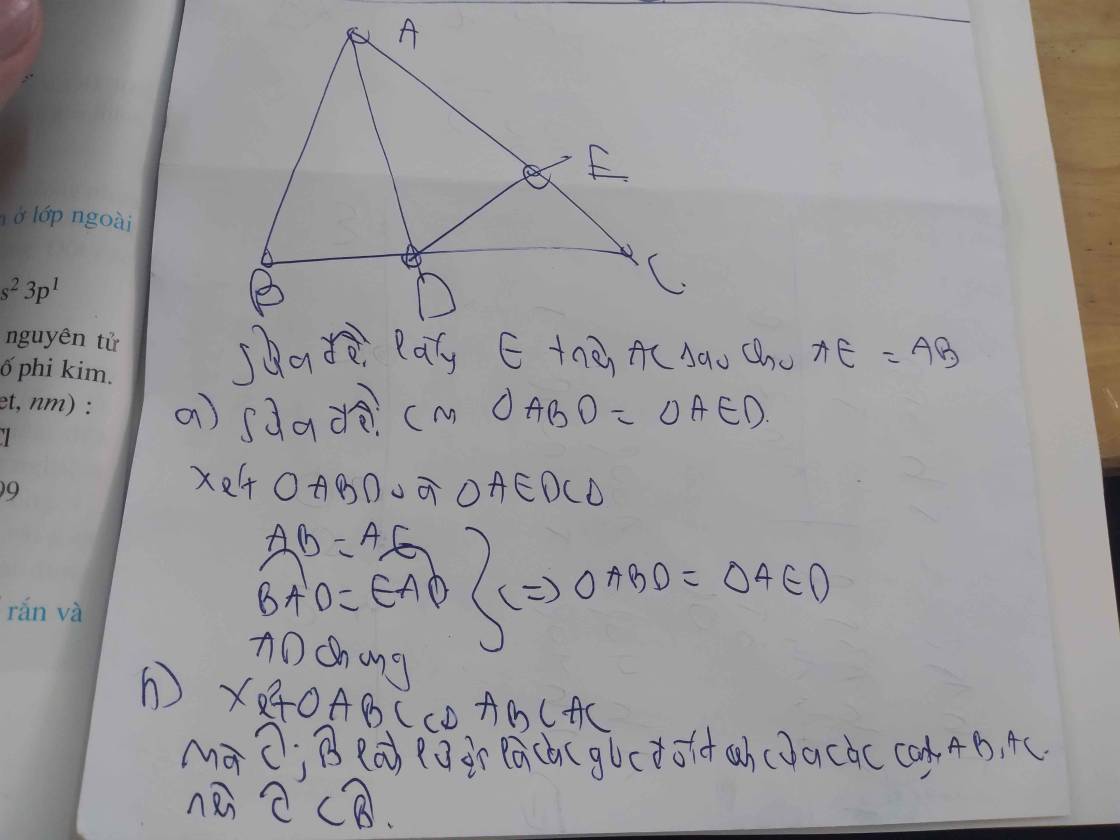
Cho tam giác ABC có góc A lớn hơn 90 độ. Lấy điểm D thuộc AB,điểm E thuộc AC. So sánh DE và BC

Những câu hỏi liên quan
Tam giác ABC có góc A = 90 độ , lấy D thuộc AB , E thuôc AC . So sánh DE và BE , DE và BC
Cho tam giác ABC có góc A=90 độ, AB<AC. Vẽ phân giác BD ( D thuộc AC). Lấy điểm E trên tia BA sao cho BE = BC
a. Chứng minh DE=DC
b. Chứng minh BD<BC
c. Lấy điểm M trên đoạn thẳng AB. So sánh DM với DB
Xét \(\Delta DBC\) và \(\Delta DBE:\)
BD chung.
BE = BC (gt).
\(\widehat{CBD}=\widehat{EBD}\) (BD là phân giác\(\widehat{B}\)).
\(\Rightarrow\) \(\Delta DBC=\Delta DBE\left(c-g-c\right).\)
\(\Rightarrow DC=DE\) ( cạnh tương ứng).
Đúng 3
Bình luận (0)
cho tam giác abc có góc a = 90 độ . tia phân giác bd của góc b ( d thuộc ac ) . trên bc lấy điểm e sao cho be = ba
a, so sánh ad và de
b, chứng minh góc edc = abc
c, chứng minh ae vuông góc với bd
a) Xét ΔABD và ΔEBD có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔABD=ΔEBD(c-g-c)
Suy ra: DA=DE(hai cạnh tương ứng) và \(\widehat{BAD}=\widehat{BED}\)(hai góc tương ứng)
mà \(\widehat{BAD}=90^0\)(gt)
nên \(\widehat{BED}=90^0\)
hay DE⊥BC
Ta có: DA=DE(cmt)
mà DE<DC(ΔDEC vuông tại E có DC là cạnh huyền)
nên DA<DC
b) Ta có: ΔBAC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)(1)
Ta có: ΔEDC vuông tại E(cmt)
nên \(\widehat{EDC}+\widehat{C}=90^0\)(hai góc nhọn phụ nhau)(2)
Từ (1) và (2) suy ra \(\widehat{ABC}=\widehat{EDC}\)(đpcm)
c) Ta có: BA=BE(gt)
nên B nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: DA=DE(cmt)
nên D nằm trên đường trung trực của AE(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (3) và (4) suy ra BD là đường trung trực của AE
hay BD\(\perp\)AE(đpcm)
Đúng 1
Bình luận (0)
bài 4: cho tam giác ABC cân tại A ( góc A nhỏ hơn 90 độ và AB nhỏ hơn BC) kẻ BD là tia phân giác của góc ABC (D thuộc AC ). Trên cạnh BC lấy điểm E sao cho AB = BE
a, vẽ hình
b,chứng minh tam giác ABD= tam giác EBD từ đó suy ra AD=DE
c,so sánh AD và DC
b: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>góc BED=90 độ và DA=DE
c: DA=DE
DE<DC
=>DA<DC
Đúng 0
Bình luận (0)
cho tam giác ABC có GÓC a = 90 độ, tia phân giác BD của góc b ( D thuộc AC ). trên cạnh BC lấy điểm E sao cho BE = BA A) so sánh đọ dài các đoạn ada và de; so sánh góc edc và abc b) chứng minh AE vuông góc Bd (giúp với)
a) Xét tam gics BAD và BED ta có:
BD là cạnh chung (gt)
AB=AE (gt)
Góc ABD=góc DBC ( vid BD là phân giác của gốc B)
=> Tam giác BAD=tam gics BED (c.g.c)
=>AD=DE ( 2 cạnh tương ứng)
=> Tam giác BAD= tam giác BED
=> góc BAD=BED(2 góc tương ứng)
=>BED=BAD=90*
Xét tam giác ABC và EDC ta cosL'
BAC=DEC=90*
góc C chung
=> tam giác ABC~tam giác EDC (g-g)
=> goác ABC=EDC
b) Xét tam giác ABE ta có:
AB=BE
=> tam giác ABE cân tại B
mà BD là tia phân giác của góc B
=> BD là đường cao
=> BD vuông góc vs AE
Đúng 1
Bình luận (0)
phần 2 câu a bạn sai rồi
Giải
có góc abc + góc c =900(tam giác abc vuông tại a)
Mà góc edc + góc c =900(tam giác edc vuông tại d)
Vậy góc abc = góc edc
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tam giác ABC có GÓC a = 90 độ, tia phân giác BD của góc b ( D thuộc AC ). trên cạnh BC lấy điểm E sao cho BE = BA A) so sánh đọ dài các đoạn ada và de; so sánh góc edc và abc b) chứng minh AE vuông góc Bd ( giúp với )
*Tự vẽ hình
a) Xét tam giác ABD và EBD có :
\(\widehat{ABD}=\widehat{DBE}\left(gt\right)\)
BD : cạnh chung
BA=BE(gt)
=> Tam giác ABD=EBD(c.g.c)
=> AD=DE
và \(\widehat{BAD}=\widehat{DEB}=90^o\)
\(\Rightarrow\widehat{BAD}=\widehat{DEC}=90^o\)
b) Gọi giao điểm của BD và AE là O
Tam giác ABO=EBO(c.g.c) (tự cm)
=> \(\widehat{BOA}=\widehat{BOE}\)
Mà : \(\widehat{BOA}+\widehat{BOE}=180^o\)
\(\Rightarrow\widehat{BOA}=90^o\)
\(\Rightarrow AE\perp BD\left(đccm\right)\)
#H
Cho tam giác ABC có góc A nhỏ hơn 90 độ. Trên cạnh AB lấy điểm D
a) So sánh các đoạn thẳng CA,CD,CB.
b) Trên cạnh AC lấy điểm E. So sánh DE và BC.
HELP T.T
Cho tam giác ABC . Góc A = 90 độ: tia phân giác BD của góc B(D thuộc AC). Trên cạnh BC lấy điểm E sao cho BE=BA
a. so sánh ad và de (khỏi vẽ hình cx dc vì mình vẽ dc r)
Để so sánh AD và DE, chúng ta cần tìm hiểu về các đặc điểm của tam giác ABC và các điểm B, D, E.
Với tam giác ABC, góc A bằng 90 độ và tia phân giác BD của góc B (D thuộc AC). Trên cạnh BC, ta lấy điểm E sao cho BE bằng BA.
Để so sánh AD và DE, chúng ta cần biết thêm về vị trí của các điểm A, B, C, D, E trên đường thẳng AC và BC.
Đúng 0
Bình luận (0)
Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
=>DA=DE
Đúng 0
Bình luận (0)
Cho ABC có ( AB < AC) và AD là phân giác của A (DE BC). Gọi E là một điểm bất kỳ thuộc cạnh AD(E khác A;D). Trên cạnh AC lấy điểm F sao cho AF = AB . a) Chứng minh: tam giác ABE = tam giác AFE.
b) So sánh các góc B.và C. So sánh AD và AC biết ADC = 105°