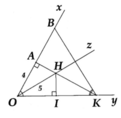
Cho góc nhọn xOy. Trên Ox lấy điểm A, trên Oy lấy điểm B sao cho OA = \(\frac{1}{2}\)OB. Hạ \(AH\perp Oy\), \(BK\perp Ox\)(\(H\in Oy\), \(K\in Ox\)). Tia phân giác Ot của góc xOy cắt BK tại P. Đường thẳng vuông góc với OP tại O cắt đường thẳng AH tại C. Đường thẳng HK cắt OC tại Q. CMR:
a. \(\frac{PK}{PB}=\frac{CH}{CA}\)
b. HQ = HK.