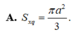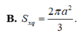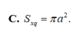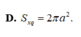Cạnh bên của một tam giác cân bằng 13,6 cm Góc ở đáy bằng 30 độ
aTính độ dài đường tròn và diện tích hình tròn ngoại tiếp tam giác cân đó
bTính diện tích hai hình viên phân ứng với hai cạnh bên
Những câu hỏi liên quan
cho hình chóp tam giác đều SABC có cạnh đáy bằng a cạnh bên hợp với đáy một góc 60 độ hình nón tròn xoay có đỉnh s đáy là đường tròn ngoại tiếp tam giác ABC có diện tích xung quanh là
Xem chi tiết
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABC\right)\Rightarrow\widehat{SAO}=60^0\)
\(AO=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\)
\(SA=\dfrac{AO}{cos60^0}=\dfrac{2a\sqrt{3}}{3}\)
\(S_{xq}=\pi.AO.SA=\dfrac{2\pi a^2}{3}\)
Đúng 2
Bình luận (0)
1, góc ở đỉnh của một tam giác cân bằng 78 độ , cạnh đáy dài 28,5cm. Tính cạnh bên và diện tích tam giác
2 ,cạnh bên của một tam giác cân dài 17,2cm. góc ở đáy của tam giác cân là 46 độ. Tính cạnh đáy và diện tích tam giác
. Giúp mình với ạ!! Cảm ơn nhìu ạ
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và cạnh bên bằng 2a Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai tam giác ABC và A’B’C’ Diện tích xung quanh của hình trụ bằng A.
4
3
π
a
2
3
B.
2...
Đọc tiếp
Cho hình lăng trụ tam giác đều ABC.A’B’C’ có cạnh đáy bằng a và cạnh bên bằng 2a Một hình trụ có hai đáy là hai hình tròn ngoại tiếp hai tam giác ABC và A’B’C’ Diện tích xung quanh của hình trụ bằng
A. 4 3 π a 2 3
B. 2 3 π a 2 3
C. 4 π a 2
D. 2 π a 2
1. Tính diện tích của một hình thang cân biết hai đáy là 12 cm và 18 cm Góc ở đáy là 75 Độ
2. Tính diện tích của một hình bình hành có hai cạnh là 12 cm và 15 cm góc tạo bởi 2 cạnh ấy là 110 độ
3. Cho tam giác ABC góc A bằng 75 Độ AB bằng 30 cm BC = 35 cm Tính AC và dịch tiếp tam giác abc
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.Câu 2: Cho hình thang cân ABCD, đáy lớn CD10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.Câu 4: Cho tam giác ABC vuông tại A, ABAC; gọi I là giao điểm các đường phân giác, M là...
Đọc tiếp
Câu 1:Tính độ dài cạnh AB của tam giác ABC vuông tại A có hai đường trung tuyến AM và BN lần lượt bằng 6 cm và 9 cm.
Câu 2: Cho hình thang cân ABCD, đáy lớn CD=10 cm, đáy nhỏ bằng đường cao, đường chéo vuông góc với cạnh bên. Tính độ dài đường cao của hình thang cân đó.
Câu 3: Cho tam giác ABC cân tại A, đường cao ứng với cạnh đáy có độ dài 15,6 cm, đường cao ứng với cạnh bên dài 12 cm. Tính độ dài cạnh đáy BC.
Câu 4: Cho tam giác ABC vuông tại A, AB<AC; gọi I là giao điểm các đường phân giác, M là trung điểm BC . Cho biết góc BIM bằng 90°. Tính BC:AC:AB.
Câu 1: Tam giác ABC vuông tại A có AM là đường trung tuyến ứng với cạnh huyền BC
=> AM=\(\frac{1}{2}\)BC mà AM=6 cm=> BC=12cm.
Tam giác ANB vuông tại A có AN2+AB2=BN2 (Theo Pytago) mà BN=9cm (gt)
=>AN2+AB2=81 Lại có AN=\(\frac{1}{2}\)AC =>\(\frac{1}{2}\)AC2+AB2=81 (1)
Tam giác ABC vuông tại A có: AC2+AB2=BC2 => BC2 - AB2 = AC2 (2)
Từ (1) và (2) suy ra \(\frac{1}{4}\)* (BC2 - AB2)+AB2=81 mà BC=12(cmt)
=> 36 - \(\frac{1}{4}\)AB2+AB2=81
=> 36+\(\frac{3}{4}\)AB2=81
=> AB2=60=>AB=\(\sqrt{60}\)
Đúng 1
Bình luận (0)
C2
Cho hình thang cân ABCD có đáy lớn CD = 1
C4
Câu hỏi của Thiên An - Toán lớp 9 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
một hình vuông với chiều dài một cạnh bên là 8cm và một tam giác cân với chiều dài cạnh đáy là 12cm. nếu diện tích hình vuông bằng diện tích tam giác cân thì chiều cao của tam giác cân là bao nhiêu?
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng
60
∘
. Tính diện tích xung quanh của hình nón đỉnh S, có đáy là hình tròn ngoại tiếp tam giác ABC A.
πa
2
10
8
B.
πa
2
3
3...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 60 ∘ . Tính diện tích xung quanh của hình nón đỉnh S, có đáy là hình tròn ngoại tiếp tam giác ABC
A. πa 2 10 8
B. πa 2 3 3
C. πa 2 7 4
D. πa 2 7 6
một tam giác cân có cạnh đáy 16cm, cạnh bên 10cm. Tính độ dài các bán kính đường tròn nội tiếp, ngoại tiếp tam giác và khoảng cách giữa các tâm của hai đường tròn đó
Cho S.ABC là hình chóp tam giác đều, cạnh đáy là a, cạnh bên hợp với mặt đáy góc
60
∘
. Tính diện tích xung quanh của hình nón tròn xoay có đỉnh S, đáy là đường tròn ngoại tiếp tam giác ABC.
Đọc tiếp
Cho S.ABC là hình chóp tam giác đều, cạnh đáy là a, cạnh bên hợp với mặt đáy góc 60 ∘ . Tính diện tích xung quanh của hình nón tròn xoay có đỉnh S, đáy là đường tròn ngoại tiếp tam giác ABC.
