Cho tam giác ABC có các đường cao BD,CE cắt nhau tại H. CMR:
A) góc HBC= góc HED
B) Gọi I là trung điểm của BC. Đường thẳng vuông góc với HI tại H. CM MH vuông góc BD
Cho tam giác ABC có các đường cao BD,CE cắt nhau tại H. CMR:
A) góc HBC= góc HED
B) Gọi I là trung điểm của BC. Đường thẳng vuông góc với HI tại H. CM MH vuông góc BD
Cho tam giác nhọn ABC có các đường cao BD, CE cắt nhau tại H. Gọi I là trung điểm của BC. Đường vuông góc với HI tại H cắt AB tại M. Gọi N là điểm đối xứng với A qua H. Chứng minh rằng:BD vuông với MN
Cho tam giác ABC có 3 góc nhọn, các đường cao BD và CE cắt nhau tại H. Qua B kẻ đường thẳng vuông góc với Ab tại B, qua C kẻ đường thẳng vuông góc với AC tại C, chúng cắt nhau tại K. Gọi M là trung điểm của BC
a) Chứng minh: H, M, K thẳng hàng
b) Tam giác ABC thỏa mãn điều kiện gì để tứ giác BHCK là hình thoi
c) Gọi O là trung điểm của AK, CH giao với MA tại G. Chứng minh: G là trọng tâm của tam giác ABC
a: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>H,M,K thẳng hàng
b: BHCK là hình thoi khi BH=HC
=>AB=AC
Bài 7: Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H .Đường vuông góc với AB tại B
và đừơng vuông góc với AC tại C cắt nhau tại K.Gọi M là trung điểm của BC.
Chứng minh rằng :
a) ADB ∼
AEC; AED ∼
ACB.
b) HE.HC = HD. HB
c) H,M,K thẳng hàng
d) Tam giác ABC phải có điều kiện gì thì tứ giác BACK sẽ là hình thoi? Hình chữ nhật?
Bài 8:Cho tam giác ABC cân tại A , trên BC lấy điểm M.Vẽ ME , MF vuông góc với AC,AB,Kẻ
đường cao CA . CMR:
a) Tam giác BFM đồng dạng với tam giác CEM.
b) Tam giác BHC đồng dạng với tam giác CEM.
c) ME + MF không thay đổi khi M di động trên BC.
cho tam giác abc, các đường cao bd, ce cắt nhau tại h. đường vuông góc với ab tại b và đường vuông góc ac tại c cắt nhau ở k. gọi m là trung điểm của bc
a, cm tam giác adb đồng dạng tam giác aec
b, cm he.hc=hd.hb
c, cm h, k, m, thẳng hàng
d, tam giác abc phải có điều kiện gì thì tam giác bhck là hình thoi? hình chữ nhật?
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)
c: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>M là trung điểm của HK
=>H,M,K thẳng hàng
d: BACK là hình thoi
=>M là trung điểm của AK và AK vuông góc BC
=>A,H,M thẳng hàng
=>ΔABC cân tại A
=>AB=AC
tham khảo
a.Ta có BK//CH(⊥AB),CK//BH(⊥AC)BK//CH(⊥AB),CK//BH(⊥AC)
→BHCK→BHCK là hình bình hành
b.Vì BHCKBHCK là hình bình hành
→HK∩BC→HK∩BC tại trung điểm mỗi đường
Do MM là trung điểm BCBC
→M→M là trung điểm HKHK
→H,M,K→H,M,K thẳng hàng
c.Ta có O,MO,M là trung điểm AK,HKAK,HK
→OM→OM là đường trung bình ΔAHKΔAHK
→OM//AH→OM//AH
Do BD∩CE=H→HBD∩CE=H→H là trực tâm ΔABC→AH⊥BCΔABC→AH⊥BC
→OM⊥BC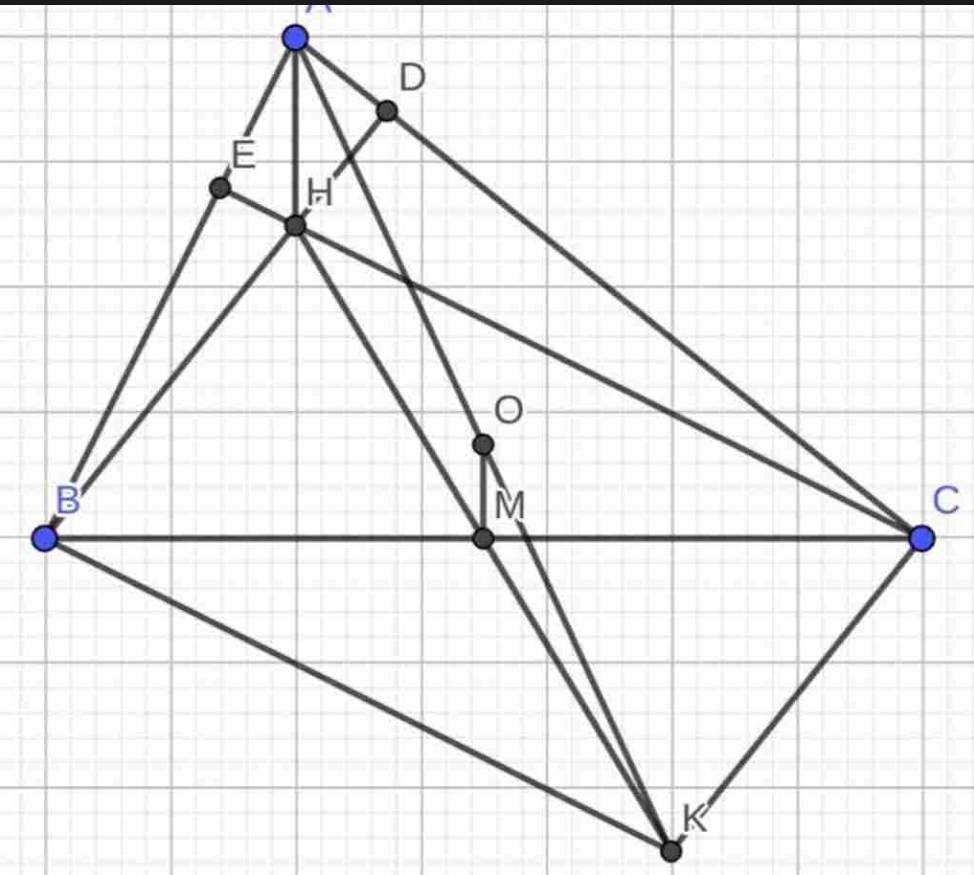
Cho tam giác ABC nhọn, các đường cao BD và CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau tại K. Gọi M là trung điểm BC. AH cắt BC tại O. CMR: H là giao điểm các đường phân giác của tam giác ODE.
Cho tam giác ABC nhọn (AB<AC), đường cao BD và CE cắt nhau tại H. Gọi I là trung điểm của BC. Từ B kẻ đường thẳng song song với CH, đường thẳng này cắt tia HI tại K. Chừng minh:
a) KC vuông góc với AC
b) Gọi F là trung điểm của AK. Chứng minh FI vuông góc với BC và FI=1/2 AH