Nêu cách xác định vị trí của một vật trên một đường thẳng

Những câu hỏi liên quan
Nêu cách xác định vị trí của một vật trên một mặt phẳng .
+ Chọn một điểm ( một vật) cố định làm mốc.
+ Một hệ trục gồm Ox và Oy vuông góc với nhau, gắn với vật mốc.
+ Chiếu vuông góc điểm vị trí vật xuống hai trục Ox và Oy.
Vị trí của bật trên mặt phẳng được xác định bằng hai tọa độ x và y.
Đúng 0
Bình luận (0)
Nêu các cách xác định vị trí của một vật trên một mặt phẳng.
Có thể xác định vị trí một vật ( một điểm ) trong mặt phẳng bằng các xác định tọa độ của nó .Ta có thể sử dụng :
-Hệ trục tọa độ vuông góc ( tọa độ Đề -Các) để xác định tọa độ 1 điểm theo theo khoảng cách so với trục X,Y hoặc
- Hệ tọa độ cực , xác định tọa độ 1 điểm theo góc ( so với trục hoành) và khoảng cách ( so với điểm chuẩn (điểm gốc))
Đúng 0
Bình luận (0)
Để xác định vị trí của vật trên mặt phẳng ta chọn hệ trục oxy. Rồi xác định tọa độ của vật trên hệ tọa độ.
Đúng 0
Bình luận (0)
Nêu cách xác định vị trí của một ô tô trên một quốc lộ.
Dựa vào cột cây số trên quốc lộ: khi ôtô đến cột cây số, ta sẽ biết vị trí ô tô cách mốc (địa điểm sẽ đến ) còn bao nhiêu km.
Đúng 0
Bình luận (0)
Nêu cách xác định vị trí của một ô tô trên quốc lộ.
Đườngquốc lộ xem như là1 đường thẳng1 chiều.
Chọn trục Ox cùng phương với đườngquốc lộ. Hướng và gốc tọa độ tùy ý.
Từ đóxác định vị trí của ô tô so với O.
Đúng 0
Bình luận (0)
Ta chọn một điểm là vật mốc (ví dụ như cột cây số). Đo khoảng cách từ cột mốc đến chiếc ô tô trên quốc lộ. Từ đó, ta xác định được vị trí của ô tô
Đúng 0
Bình luận (0)
Một vật sáng AB đặt thẳng góc với trục chính của một thấu kính hội tụ (tiêu cự 20cm) có ảnh cách vật 90cm. Xác định vị trí của vật, vị trí và tính chất của ảnh.
Sơ đồ tạo ảnh:
![]()
Khoảng cách giữa vật và ảnh qua thấu kính L = |d + d'|

Từ (1) và (2) ta có hệ phương trình:

Mặt khác, áp dụng công thức về vị trí ảnh – vật:
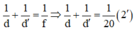
Từ (1’) và (2’) ta có hệ phương trình:

Đúng 0
Bình luận (0)
Một thấu kính hội tụ có tiêu cự 6cm. Vật sáng AB là một đoạn thẳng đặt vuông góc với trục chính của thấu kính cho ảnh ở trên màn cách vật 25cm. Xác định vị trí vật và ảnh.
Sơ đồ tạo ảnh:
![]()
Khoảng cách giữa vật và ảnh qua thấu kính

Từ (1) và (2) ta có hệ phương trình:
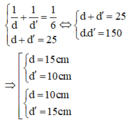
Đúng 1
Bình luận (0)
Một vật sáng AB = 4 mm đặt thẳng góc với trục chính của một thấu kính hội tụ (có tiêu cự 40cm), cho ảnh cách vật 36cm. Xác định vị trí, tính chất và độ lớn của ảnh và vị trí của vật.
Sơ đồ tạo ảnh:

Khoảng cách giữa vật và ảnh qua thấu kính L = |d + d'|
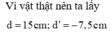
Mặt khác, áp dụng công thức về vị trí ảnh – vật:

Mặt khác, áp dụng công thức về vị trí ảnh – vật:

Vì vật là vật thật d > 0 nên ta có 2 nghiệm thỏa mãn bài toán:
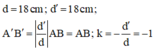
Như vậy ở trường hợp này ảnh thật cao bằng vật, ngược chiều với vật.
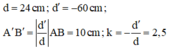
Như vậy ở trường hợp này ảnh ảo cao 10cm, cùng chiều với vật.
Đúng 0
Bình luận (0)
Một điểm sáng nằm trên trục chính của một thấu kính phân kỳ (tiêu cự bằng 15cm) cho ảnh cách vật 7,5cm. Xác định tính chất, vị trí của vật, vị trí và tính chất của ảnh.
Sơ đồ tạo ảnh:
![]()
Khoảng cách giữa vật và ảnh qua thấu kính L = |d + d'|
Vì vật thật qua thấu kính phân kì luôn luôn cho ảnh ảo nằm trong khoảng giữa vật và kính nên

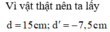
Đúng 0
Bình luận (0)
Một con lắc đơn có sợi dây dài 1m và vật nặng có khối lượng 500g. Kéo vật lệch khỏi vị trí cân bằng sao cho cho dây làm với đường thẳng đứng một góc 60o rồi thả nhẹ. Lấy
g
10
(
m
/
s
2
)
a. Xác định cơ năng của con lắc đơn trong quá trình chuyển độngb. Tính vận tốc của con lắc khi nó đi qua vị trí mà dây làm với đường thẳng đứng góc
3...
Đọc tiếp
Một con lắc đơn có sợi dây dài 1m và vật nặng có khối lượng 500g. Kéo vật lệch khỏi vị trí cân bằng sao cho cho dây làm với đường thẳng đứng một góc 60o rồi thả nhẹ. Lấy g = 10 ( m / s 2 )
a. Xác định cơ năng của con lắc đơn trong quá trình chuyển động
b. Tính vận tốc của con lắc khi nó đi qua vị trí mà dây làm với đường thẳng đứng góc 30 0 ; 45 0 và xác định lực căng của dây ở hai vị trí đó. Lấy g=10m/s2
c. Xác định vị trí để vật có v= 1,8 m/s
d. Ở vị trí vật có độ cao 0,18m vật có vận tốc bao nhieu
e. Xác định vận tốc tại vị trí 2 w t = w đ
f. Xác định vị trí để 2 w t = 3 w đ , tính vận tốc và lực căng khi đó
Chọn mốc thế năng ở vị trí cân bằng
a. Ta có cơ năng
W = m g z = m g l ( 1 − cos 60 0 ) = 0 , 5.10.1 ( 1 − 0 , 5 ) = 2 , 5 ( J )
b. Theo định luật bảo toàn cơ năng
W A = W B ⇒ m g z A = 1 2 m v B 2 + m g z B ⇒ v B = 2 g ( z A − z B ) ( 1 ) M à z A = H M = l − O M = l − l cos α 0 z B = l − l cos α
Thay vào ( 1 ) ta có
v B = 2 g l ( cos α − cos α 0 ) + K h i α = 30 0 ⇒ v B = 2 g l ( cos 30 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 3 2 − 1 2 ) ≈ 2 , 71 ( m / s )
+ K h i α = 45 0 ⇒ v B = 2 g l ( cos 45 0 − cos 60 0 ) ⇒ v B = 2.10.1 ( 2 2 − 1 2 ) ≈ 2 , 035 ( m / s )
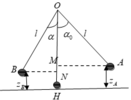
Xét tai B theo định luật II Newton ta có: P → + T → = m a →
Chiếu theo phương của dây
T − P y = m a h t ⇒ T − P cos α = m v 2 l ⇒ T − m g cos α = 2 m g ( cos α − cos α 0 ) ⇒ T = m g ( 3 cos α − 2 cos α 0 )
Khi α = 30 0 ⇒ T = m g ( 3 cos 30 0 − 2 cos 60 0 )
⇒ T = 0 , 5.10 ( 3. 3 2 − 2. 1 2 ) = 7 , 99 ( N )
Khi α = 45 0 ⇒ T = m g ( 3 cos 45 0 − 2 cos 60 0 )
⇒ T = 0 , 5.10 ( 3. 2 2 − 2. 1 2 ) = 5 , 61 N
Lưu ý: Khi làm trắc nghiệm thì các em áp dụng luôn hai công thức
+ Vận tốc của vật tại vị trí bất kỳ: v B = 2 g l ( cos α − cos α 0 )
+ Lực căng của sợi dây: T = m g ( 3 cos α − 2 cos α 0 )
c. Gọi C là vị trí để vật có v= 1,8m/s
Áp dụng công thức v C = 2 g l ( cos α − cos α 0 )
1 , 8 = 2.10.1 ( cos α − cos 60 0 ) ⇒ cos α = 0 , 662 ⇒ α = 48 , 55 0
Vật có đọ cao
z C = l − l cos α = 1 − 1.0 , 662 = 0 , 338 ( m )
d. Gọi D là vị trí vật có độ cao 0,18m
Áp dụng công thức
z D = l − l cos α ⇒ 0 , 18 = 1 − 1. cos α ⇒ cos α = 0 , 82
Áp dụng công thức
v D = 2 g l ( cos α − cos α 0 ) = 2.10.1. ( 0 , 82 − 0 , 5 ) = 2 , 53 ( m / s )
e. Gọi E là vị trí mà 2 w t = w đ Theo định luật bảo toàn cơ năng W A = W E
W A = W d E + W t E = 3 2 W d E ⇒ 2 , 5 = 3 2 . 1 2 . m v E 2 ⇒ v E = 2 , 5.4 3. m = 10 3.0 , 5 = 2 , 581 ( m / s )
f. Gọi F là vị trí để 2 w t = 3 w đ
Theo định luật bảo toàn cơ năng W A = W F
W A = W d F + W t F = 5 3 W t F ⇒ 2 , 5 = 5 3 . m g z F ⇒ z F = 2 , 5.3 5. m . g = 0 , 3 ( m ) M à z F = l − l cos α F ⇒ 0 , 3 = 1 − 1. cos α F ⇒ cos α F = 0 , 7 ⇒ α F = 45 , 573 0
Mặt khác v F = 2 g l ( cos α F − cos 60 0 ) = 2.10.1 ( 0 , 7 − 0 , 5 ) = 2 ( m / s )
Xét tại F theo định luật II Newton P → + T → = m a →
Chiếu theo phương của dây
− P cos α F + T F = m v F 2 l ⇒ − 0 , 5.10.0 , 7 + T F = 0 , 5. 2 2 1 ⇒ T = 5 , 5 ( N )
Đúng 0
Bình luận (0)









