cho tam giác ABC có góc A=80độ,góc C=40độ,trên tia đối của tiaCB lấy điểm D.CMR:AD>AC
Những câu hỏi liên quan
Cho tam giác ABC có góc A=40độ; góc C=80độ. Trên cạnh AB lấy điểm M, qua M kẻ đường thẳng song song với BC cắt AC tại N. Khi đó góc BMN=...
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tiaCB lấy điểm N sao cho BM CN.a) CMR tam giác AMN là tam giác cânb) Kẻ BH vuông góc với AM (H thuộc AM), kẻ CK vuông góc với AN (K thuộc AN). CMR : BH CK.c) CMR: AH AK.d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao ?e) Cho tam giác ABH vuông tại H, biết AB 13 cm, AH 12 cm.Tính độ dài cạnh BH ?f) Chứng minh HK // MNg) Gọi I là trung điểm của BC. Chứng minh 3 điểm A,...
Đọc tiếp
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia
CB lấy điểm N sao cho BM = CN.
a) CMR tam giác AMN là tam giác cân
b) Kẻ BH vuông góc với AM (H thuộc AM), kẻ CK vuông góc với AN (K thuộc AN). CMR : BH = CK.
c) CMR: AH = AK.
d) Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao ?
e) Cho tam giác ABH vuông tại H, biết AB = 13 cm, AH = 12 cm.Tính độ dài cạnh BH ?
f) Chứng minh HK // MN
g) Gọi I là trung điểm của BC. Chứng minh 3 điểm A, O, I thẳng hàng.
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
hay ΔAMN cân tại A
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK
c: Ta có: ΔABH=ΔACK
nên AH=AK
d: Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
BM=CN
\(\widehat{M}=\widehat{N}\)
Do đó: ΔHBM=ΔKCN
Suy ra: \(\widehat{HBM}=\widehat{KCN}\)
mà \(\widehat{HBM}=\widehat{OBC}\)
và \(\widehat{KCN}=\widehat{OCB}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
Đúng 1
Bình luận (0)
Cho tam giác ABC, có góc B+ góc C= 60 độ, phân giác AD. Trên AD lấy điểm O. Trên tia đối của tia AC lấy điểm M sao cho góc ABM= góc ABO. Trên tia đối của AB lấy điểm N sao cho góc ACN= góc ACO. CMR:
a, AM=AN
b, Tam giác MON đều
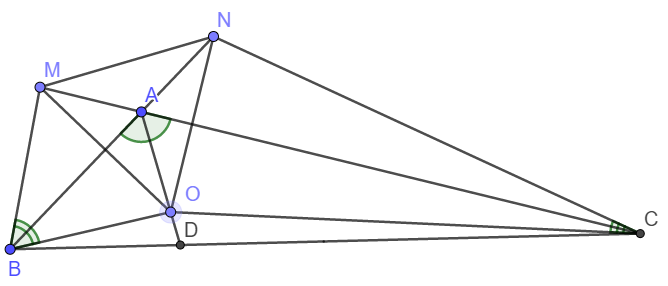
a) Xét tam giác ABC có ˆB+ˆC=60o⇒BAC=120oB^+C^=60o⇒BAC=120o
Do AD là phân giác nên ˆBAD=ˆCAD=60oBAD^=CAD^=60o
ˆMABMAB^ và ˆBACBAC^ là hai góc kề bù nên ˆMAB=180o−120o=60oMAB^=180o−120o=60o
Vậy thì ΔMAB=ΔOAB(g−c−g)ΔMAB=ΔOAB(g−c−g)
⇒AM=AO⇒AM=AO
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do ΔMAB=ΔOAB⇒AM=AO;BM=BOΔMAB=ΔOAB⇒AM=AO;BM=BO
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.
Đúng 1
Bình luận (0)
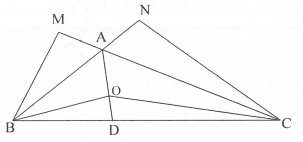Ta có: △ABC có góc B+góc C=60 độ
➩góc BAC =120 độ
ta có AD là phân giác
góc BAC=>BAD=CAD=\(\dfrac{1}{2}\)BAC=60 độ
△ABO và ΔABM có góc BAO= BAM=60 độ
AB chung
góc ABM =ABO
➩tam giác ABO =tam giác ABM (g.c.g)
➝AM=AO (*)
Ta chứng minh tương tự như trên:
tam giác ACO= tam giác ACN (g.c.g)
➝AN=AO(**)
Từ (*)(**) ⇒AM=AN (đpcm)
Đúng 1
Bình luận (0)
cho tam giác ABC có góc A= 80độ, c=50độ. trên tia đối của tia AC lấy điiểm D. vẽ góc COD bằng và so le trong với C. gọi AM là tia phân giác của góc BAD.
a) chứng minh rằng DE// AM
b) chứng minh BC//AM
Cho tam giác ABC có ABAC, đường cao BH. Từ điểm D trên cạnh BC kẻ DE vuông góc với AB, DF vuông góc với AC, DK vuông góc với BH.a) Chứng minh rằng góc KDB góc ACB.b) Chứng minh rằng tam giác EBD tam giác KDBc) Chứng minh rằng DE+ DF BHd) Trên tia đối của tia CA lấy điểm P sao cho CP HF. Chứng minh rằng trung điểm của EP nằm trên BC.e) Cho góc A 40độ, kẻ đường cao AM. Trên các đoạn thẳng AM , AC lấy điểm E, F sao cho góc ABE góc CBF 30độ. Tính góc AEF.
Đọc tiếp
Cho tam giác ABC có AB=AC, đường cao BH. Từ điểm D trên cạnh BC kẻ DE vuông góc với AB, DF vuông góc với AC, DK vuông góc với BH.
a) Chứng minh rằng góc KDB= góc ACB.
b) Chứng minh rằng tam giác EBD = tam giác KDB
c) Chứng minh rằng DE+ DF= BH
d) Trên tia đối của tia CA lấy điểm P sao cho CP = HF. Chứng minh rằng trung điểm của EP nằm trên BC.
e) Cho góc A = 40độ, kẻ đường cao AM. Trên các đoạn thẳng AM , AC lấy điểm E, F sao cho góc ABE= góc CBF = 30độ. Tính góc AEF.
cho tam giác abc có góc a=90 độ (AB>AC). Gọi I là trung điểm của đoạn thẳng AB . Trên tia đối của IC lấy điểm D sao cho IC=ID a)Chứng minh tam giác CIA = tam giác DIB b)chứng minh góc ABC = góc BAD c)trên tia đối của AC lấy điểm M sao cho AM = AB .Trên đoạn thẳng AB lấy điểm N sao cho AN=AC . Chứng minh MN vuông góc với BC
a: Xét ΔCIA và ΔDIB có
IC=ID
\(\widehat{CIA}=\widehat{DIB}\)
IA=IB
Do đó: ΔCIA=ΔDIB
Đúng 1
Bình luận (1)
Cho tan tam giác ABC có góc A bằng 100 độ góc B bàng 40độ .Trên BC lấy D trên tia đối CB lấy E sao cho BD = CE .CMR AB+AC<AD+AE
Bài 1: Cho tam giác ABC đều. Trên tia đối tia BC lấy điểm D, trên tia đối tia CB lấy điểm E sao cho BDCEBCa) C/m: tam giác ACE cânb) Tính góc DAEBài 2: Cho tam giác ABC cân tại A. Trên tia đối tia AC lấy điểm D sao cho AD AC. C/m tam giác BCD vuôngBài 3: Cho tam giác ABC cân tại A có góc A 40 độ. Lấy điểm D khác phía B so với AC thoả mãn góc CAD60 độ, góc ACD80 độ. C/m BD vuông góc AC
Đọc tiếp
Bài 1: Cho tam giác ABC đều. Trên tia đối tia BC lấy điểm D, trên tia đối tia CB lấy điểm E sao cho BD=CE=BC
a) C/m: tam giác ACE cân
b) Tính góc DAE
Bài 2: Cho tam giác ABC cân tại A. Trên tia đối tia AC lấy điểm D sao cho AD = AC. C/m tam giác BCD vuông
Bài 3: Cho tam giác ABC cân tại A có góc A= 40 độ. Lấy điểm D khác phía B so với AC thoả mãn góc CAD=60 độ, góc ACD=80 độ. C/m BD vuông góc AC
Cho tam giác ABC có góc B + góc C = 60 độ, phân giác AD,trên AD lấy điểm O, trên tia đối của tia AC lấy điểm M sao cho góc ABM = góc ABO. Trên tia đối của AB lấy điểm N sao cho góc ACN = góc ACO. CMR:
a. AM = AN
b. tam giác MON đều
a) Xét tam giác ABC có \(\widehat{B}+\widehat{C}=60^o\Rightarrow BAC=120^o\)
Do AD là phân giác nên \(\widehat{BAD}=\widehat{CAD}=60^o\)
\(\widehat{MAB}\) và \(\widehat{BAC}\) là hai góc kề bù nên \(\widehat{MAB}=180^o-120^o=60^o\)
Vậy thì \(\Delta MAB=\Delta OAB\left(g-c-g\right)\)
\(\Rightarrow AM=AO\)
Hoàn toàn tương tự ta có AN = AO
Vậy nên AM = AN.
b) Ta có do \(\Delta MAB=\Delta OAB\Rightarrow AM=AO;BM=BO\)
Suy ra AB là trung trực của MO,.
Lại có N thuộc AB nên NM = NO
Hoàn toàn tương tự ta có MO = MN
Vậy OM = ON = MN hay OMN là tam giác đều.
Đúng 2
Bình luận (0)