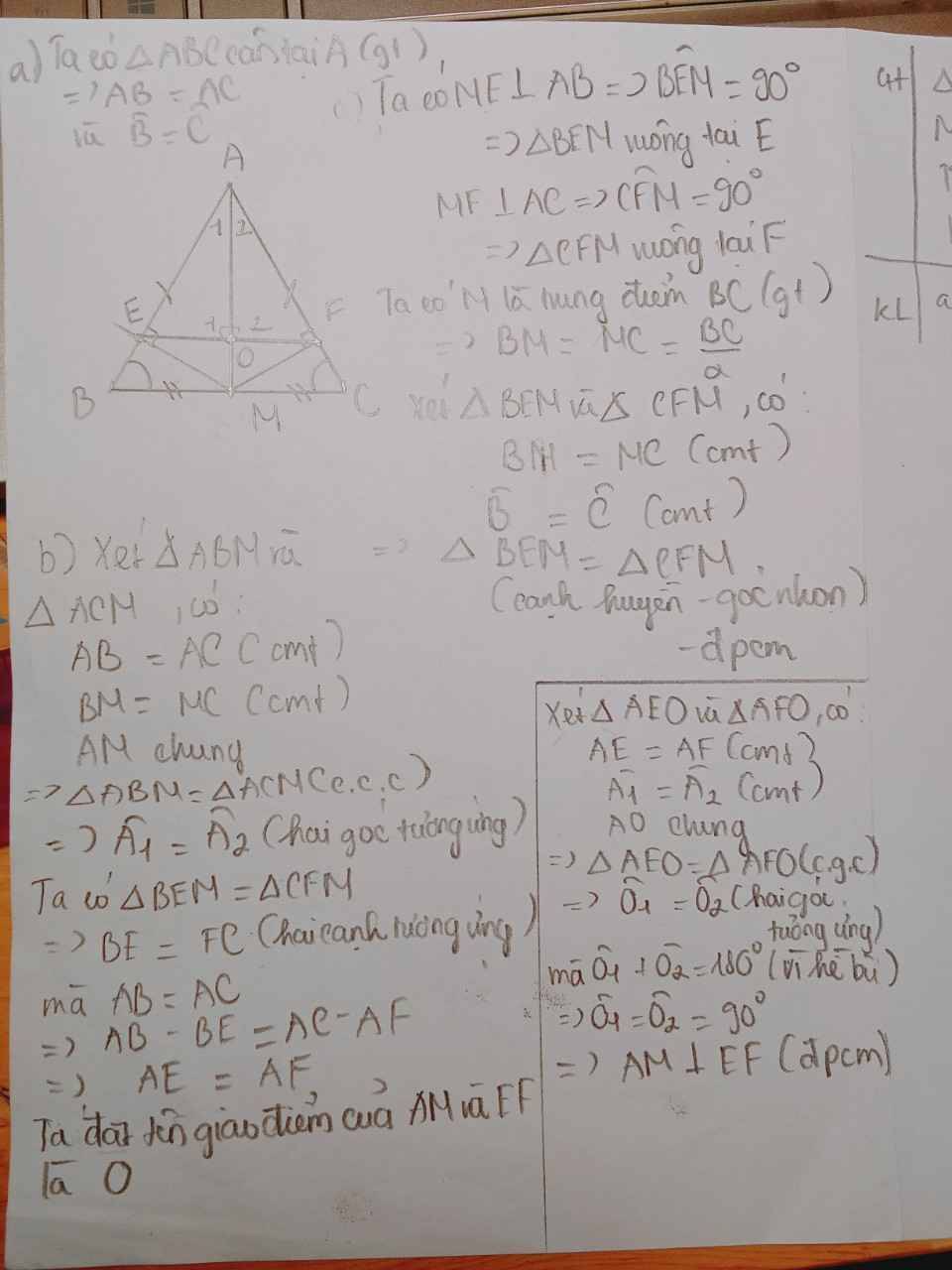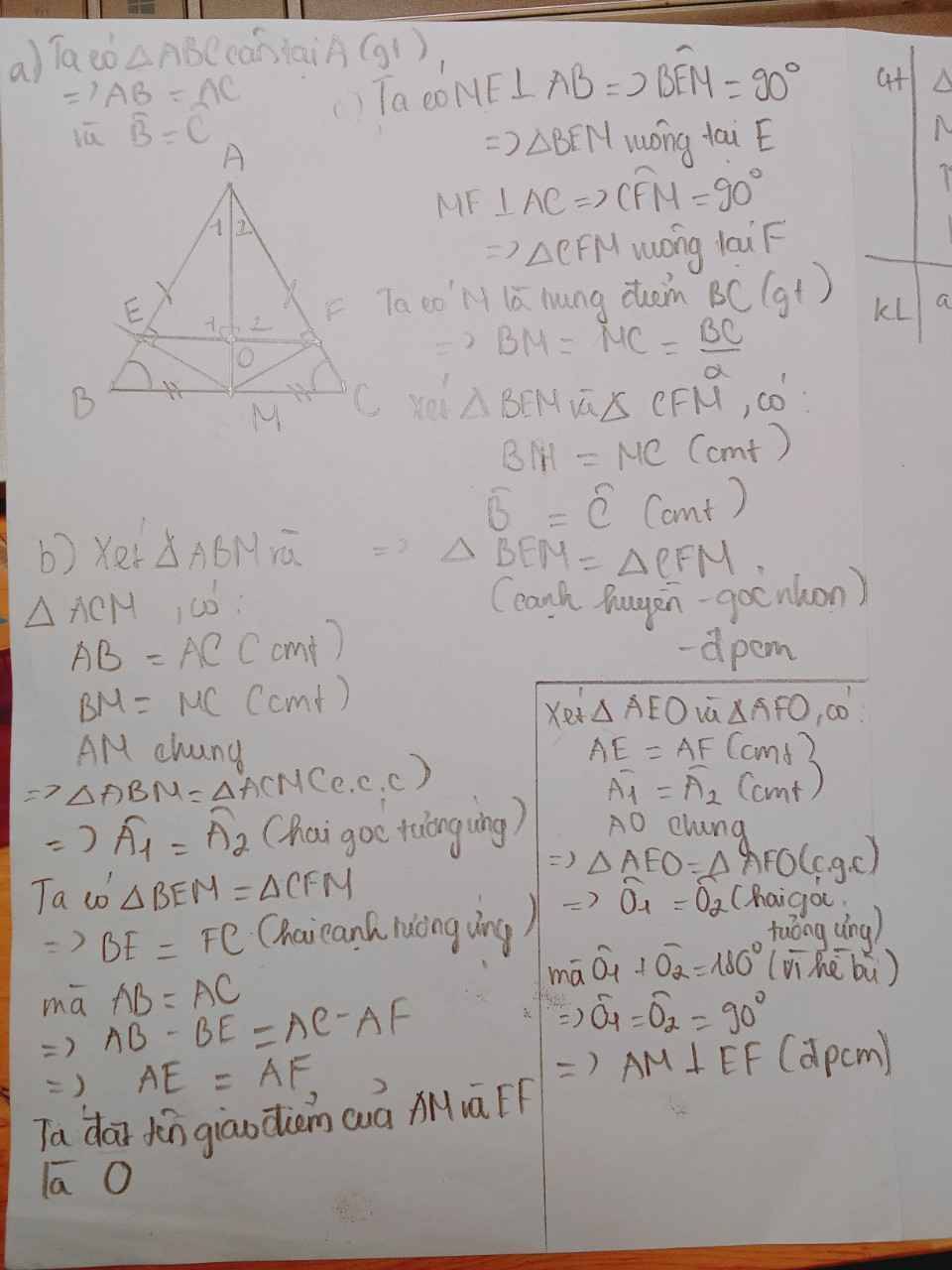Cho tam giác ABC có AM vuông góc với BC. Kẻ MD vuông góc với AB tại D. Kẻ ME vuông góc với AC tại E. Biết BD = CE, chứng minh tam giác ABC cân.

Những câu hỏi liên quan
Cho tam giác ABC cân tại A.Kẻ AM vuông góc với BC (M thuộc BC)
a) Chứng minh MB=MC
b) Chứng minh góc BAM=CAM
c) Kẻ MD vuông góc với AB ( D thuộc AB ).Kẻ ME vuông góc với AC (E thuộc AC).Chứng minh tam giác MDE là tam giác cân
Xem chi tiết
a) Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC(ΔABC cân tại A)
AM chung
Do đó: ΔAMB=ΔAMC(cạnh huyền-cạnh góc vuông)
Suy ra: MB=MC(hai cạnh tương ứng)
b) Ta có: ΔAMB=ΔAMC(cmt)
nên \(\widehat{BAM}=\widehat{CAM}\)(hai góc tương ứng)
c) Xét ΔDMB vuông tại D và ΔEMC vuông tại E có
MB=MC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔDMB=ΔEMC(cạnh huyền-góc nhọn)
Suy ra: DM=EM(hai cạnh tương ứng)
Xét ΔMDE có MD=ME(cmt)
nên ΔMDE cân tại M(Định nghĩa tam giác cân)
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A
A
^
90
°
. Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc với AB tại E.a) Chứng minh tam giác ADE cân.b) Chứng minh DE// BC.c) Gọi I là giao điểm của BD và CE. Chứng minh IB ICd) Chứng minh.
A
I
⊥
B
C
.
Đọc tiếp
Cho tam giác ABC cân tại A A ^ < 90 ° . Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc với AB tại E.
a) Chứng minh tam giác ADE cân.
b) Chứng minh DE// BC.
c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC
d) Chứng minh. A I ⊥ B C .
Câu 7. Cho tam giác MNP cân tại M. Tia phân giác của góc NMP cắt NP tại A.
a) Chứng minh tam giác AMN = tam giác AMP.
b) Kẻ AB vuông góc với MN, AC vuông góc với MP. Chứng minh tam giác ABC
cân.
c) Chứng minh AM vuông góc với BC
d) Kẻ BD vuông góc với NA tại D. Gọi E là giao điểm của đường thẳng BD và MP.
Chứng minh M là trung điểm của CE.
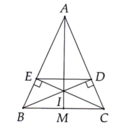
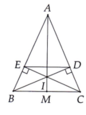
cho tam giác ABC cân tại A, M là trung điểm của BC, từ M kẻ ME vuông góc với AB tại E, kẻ ME vuông góc với AC tại F.a
a)chứng minh tam giác BEM=tam giác CFM
b)chứng minh AM vuông góc với EF
a, Xét tam giác BEM và tam giác CFM có :
Góc BEM = Góc CFM = 90 độ
MB = MC ( gt )
Góc B = Góc C ( gt )
=> Tam giác BEM = Tam giác CFM ( ch-gn )
b, Do tam giác BEM = Tam giác CFM ( câu a, )
=> EB = FC
E thuộc AB = > AE + EB = AB
=> AE = AB - EB ( 1 )
F thuộc AC = > AF + FC = AC
=> AF = AC - FC ( 2 )
(1), ( 2 ) => AE = AF
Gọi I là giao của AM và EF
AM là đg trung tuyến của tam giác ABC mà tam giác ABC cân
=> AM là đg phân giác
=> Góc EAI = Góc FAI
Xét tam giác EAI và tam giác FAI có
AE = AF ( cmt )
AI chung
Góc EAI = Góc FAI ( cmt )
=> Tam giác EAI = Tam giác FAI ( c-g-c )
=> Góc AME = Góc AMF
Mà Góc AME + Góc AMF = 180 độ ( 2 góc kề bù )
=> Góc AME = Góc AMF = 90 độ
=> AM vuông góc vs EF ( đpcm )
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A . gọi M là trung điểm của BC . kẻ BD vuông góc với AC , CE vuông góc với AB ( D thuộc AC ; E thuộc AB ) . BD cắt CE tại I . chứng minh : BE = CD và tam giác IBC cân
Xem chi tiết
cho tam giác abc có ab=ac. kẻ bd vuông góc với ac tại d kẻ ce vuông góc ab tại e. Gọi I là giao điểm của BD và CE. CA chứng minh rằng:
a) tam giác ABD= tam giác ACE
b) EI=DI
AI vuông góc với BC
cho tam giác abc cân tại a. Trên cạch BC lấy D,trên tia đối CB lấy E sao cho bd=ce. Từ D kẻ đường thảng vuông góc với BC cắt AB tại M, từ E kẻ vuông góc với BC cắt AC tại M
a, Chứng minh MD=ME
b,Gọi i là gđ MD và BE.Chứng minh I là trung điểm BE
Cho tam giác ABC cân tại A (góc A nhọn) kẻ BD vuông góc với AC tại D,kẻ CE vuông góc AB tại E
TAM GIÁC ADE CÂN,DE SONG SONG BC,BD CẮT CE TẠI I,CHỨNG MINH IB=IC AI VUÔNG GÓC BC
a: Xét ΔABD vuông tại D vaf ΔACE vuông tại E có
AB=AC
góc BAD chung
=>ΔABD=ΔACE
=>AD=AE
b: Xét ΔABC có AD/AC=AE/AB
nên DE//BC
c: Xét ΔIBC có góc ICB=góc IBC
nên ΔIBC cân tại I
d: AB=AC
IB=IC
=>AI là trung trực của BC
=>AI vuông góc BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A ( < 90 ° ). Kẻ BD vuông góc với AC tại D, kẻ CE vuông góc vói AB tại E. a) Chứng minh tam giác ADE cân. b) Chứng minh DE / / BC c) Gọi I là giao điểm của BD và CE. Chứng minh IB = IC d) Chứng minh. AI BC