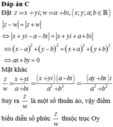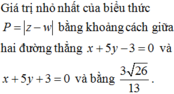w
wèwefwefwef
Đọc tiếp
wwèwefwefwef
Những câu hỏi liên quan
Mọi người cho mình hỏi chút: Thời gian từ lúc W L = W Lmax (W C = W Cmax ) đến lúc W L = W Lmax /2 (W C = W Cmax /2) là :
Bạn ơi bạn hack não người ta hả bạn(tên thì rõ đẹp mà còn chơi khăm)
Đúng 0
Bình luận (0)
Có bao nhiêu phát biểu sau là đúng (z, w là các số phức): (*)
z
w
¯
thì
z
¯
w
(*) z
-
w
¯
→
z
¯
-
w
(*)
z
3
w...
Đọc tiếp
Có bao nhiêu phát biểu sau là đúng (z, w là các số phức):
(*) z = w ¯ thì z ¯ = w
(*) z = - w ¯ → z ¯ = - w
(*) z 3 = w 3 → z = w
(*) z 6 = 1 thì có 6 nghiệm phức
(*) z = w ¯ ⇔ z , w ∈ ℝ
A. 2 phát biểu
B. 3 phát biểu
C. 4 phát biểu
D. 5 phát biểu
SGK Cánh Diều
13 tháng 8 2023 lúc 22:34
Cho \(u = u(x),\,v = v(x),\,w = w(x)\) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định. Chứng minh rằng \((u\,.\,v\,.\,w)' = u'\,.\,v\,.\,w + u\,.\,v'\,.\,w + u\,.\,v\,.\,w'\)
Đặt: \(g(x) = u(x).v(x),\,\,f(x) = g(x).w(x)\)
Ta có:
\(f'(x) = g'(x).w(x) + g(x).w'(x) = \left( {u.v} \right)'.w(x) + (uv).w'(x) = \left( {u'v + uv'} \right).w + (uv).w'\)\( = u'vw + uv'w + uvw'\)
Đúng 0
Bình luận (0)
Cộng các phân thức sau:a)
b
3
+
b
b
3
+
1
+
b
b
2
−
b
+
1
+
2
b
+...
Đọc tiếp
Cộng các phân thức sau:
a) b 3 + b b 3 + 1 + b b 2 − b + 1 + 2 b + 1 với b ≠ − 1 ;
b) 2 ( u − v ) ( u − w ) + 2 ( v − w ) ( w − u ) + 2 ( w − u ) ( u − v ) với u ≠ v ≠ w .
Cho hai số phức z và w
z
≠
0,
w
≠
0
. Biết
z
−
w
z
+
w
. Khi đó điểm biểu diễn số phức
z
w
A. thuộc trục Ox B. thuộc đường phân giác của góc phầ...
Đọc tiếp
Cho hai số phức z và w z ≠ 0, w ≠ 0 . Biết z − w = z + w . Khi đó điểm biểu diễn số phức z w
A. thuộc trục Ox
B. thuộc đường phân giác của góc phần tư thứ nhất và thứ ba.
C. thuộc trục Oy
D. thuộc đường phân giác của góc phần tư thứ hai và thứ tư
Đáp án C
Đặt z = x + y i ; w = a + b i , x ; y ; a ; b ∈ ℝ
z − w = z + w ⇔ x + y i − a − b i = x + y i + a + b i
⇔ x − a 2 + y − b 2 = x + a 2 + y + b 2 ⇔ a x + b y = 0
Mặt khác
z w = x + y i a + b i = x + y i a − b i a 2 + b 2 = − a y + b x i a 2 + b 2
Suy ra z w là một số thuần ảo, vậy điểm biểu diễn số phức z w thuộc trục Oy
Đúng 0
Bình luận (0)
Cho hai số phức z và w
z
≠
0
,
w
≠
0
. Biết
z
−
w
z
+
w
. Khi đó điểm biểu diễn số phức
z
w
A. thuộc trục Ox. B. thuộc đường phân giác của góc phần...
Đọc tiếp
Cho hai số phức z và w z ≠ 0 , w ≠ 0 . Biết z − w = z + w . Khi đó điểm biểu diễn số phức z w
A. thuộc trục Ox.
B. thuộc đường phân giác của góc phần tư thứ nhất và thứ ba.
C. thuộc trục Oy.
D. thuộc đường phân giác của góc phần tư thứ hai và thứ tư.
Cho số phức z và w thỏa mãn z+w3+4i và
z
-
w
9
. Tìm giá trị lớn nhất của biểu thức
T
z
+
w
. A. maxT
176
B. maxT14 C. maxT4 D. maxT...
Đọc tiếp
Cho số phức z và w thỏa mãn z+w=3+4i và z - w = 9 .
Tìm giá trị lớn nhất của biểu thức T = z + w .
A. maxT= 176
B. maxT=14
C. maxT=4
D. maxT= 106
Đáp án D
Đặt 
theo giả thiết ta có:
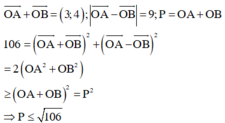
Tổng quát: Với 2 số thực
z
1
,
z
2
thõa mãn 
Khi đó 
Đúng 0
Bình luận (0)
Cho số phức z và w thỏa mãn
z
+
w
3
+
4
i
và
z
-
w
9
Tìm giá trị lớn nhất của biểu thức
T
z
+
w
Đọc tiếp
Cho số phức z và w thỏa mãn z + w = 3 + 4 i và z - w = 9 Tìm giá trị lớn nhất của biểu thức T = z + w
Xét các số phức z, w thỏa |z-1-3i| ≤ |z+2i| và |w+1+3i| ≤ |w-2i|. Giá trị nhỏ nhất của biểu thức P |z-w| là A. 3/13 B.
3
26
13
C.
26
4
D.
13
+
1
2
Đọc tiếp
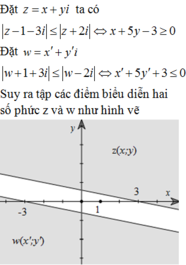
Xét các số phức z, w thỏa |z-1-3i| ≤ |z+2i| và |w+1+3i| ≤ |w-2i|. Giá trị nhỏ nhất của biểu thức P = |z-w| là
A. 3/13
B. 3 26 13
C. 26 4
D. 13 + 1 2
Cho các số phức z , w khác 0 thỏa mãn z+ w \(\ne\) 0 và \(\dfrac{1}{z}+\dfrac{3}{w}=\dfrac{6}{z+w}\) . Khi đó \(\left|\dfrac{z}{w}\right|\) bằng
A:\(\sqrt{3}\)
B: \(\dfrac{1}{\sqrt{3}}\)
C: 3
D: \(\dfrac{1}{3}\)