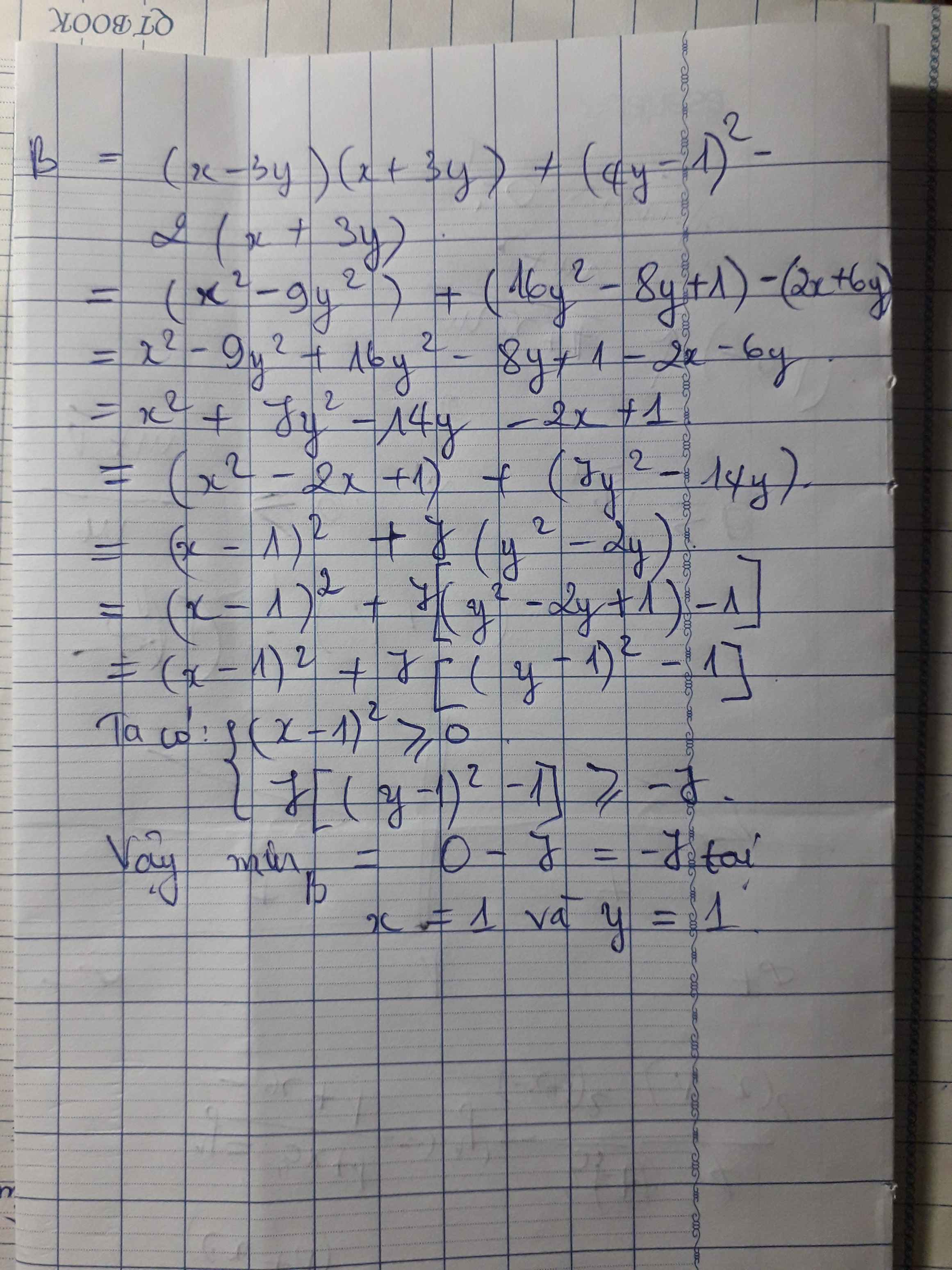a. giá trị nhỏ nhất của B=3 khi và chỉ khi x=y=1006

1/B=\(-\left(x^2+2y^2+2xy-2y\right)\)

     =\(-\left(x^2+2xy+y^2+y^2-2y+1-1\right)\)

     =\(-\left[\left(x+y\right)^2+\left(y-1\right)^2\right]+1\)<=1

Bmax=1 khi x+y=0 và y-1=0=>x=-1;y=1

2/C=\(x^2+x+\frac{1}{4}+y^2+y+\frac{1}{4}+\frac{1}{2}\)

      =\(\left(x+\frac{1}{2}\right)^2+\left(y+\frac{1}{2}\right)^2+\frac{1}{2}\)>=\(\frac{1}{2}\)

Cmin=\(\frac{1}{2}\)khi \(x+\frac{1}{2}=0\)và \(y+\frac{1}{2}=0\)=>\(x=y=\frac{-1}{2}\)

có làm mới có ăn nha em

\(A=\left(x^2+2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{5}{4}=\left(x+\dfrac{3}{2}\right)^2-\dfrac{5}{4}\ge-\dfrac{5}{4}\\ A_{min}=-\dfrac{5}{4}\Leftrightarrow x=-\dfrac{3}{2}\\ B=\left(x^2+2xy+y^2\right)+\left(x^2+6x+9\right)+3\\ B=\left(x+y\right)^2+\left(x+3\right)^2+3\ge3\\ B_{min}=3\Leftrightarrow\left\{{}\begin{matrix}x+y=0\\x+3=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\\ C=-\left(x^2-2x+1\right)+1=-\left(x-1\right)^2+1\le1\\ C_{max}=1\Leftrightarrow x=1\)

\(x^2+2xy+6x+6y+2y^2+8=0\)

\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(6x+6y\right)+9+y^2-1=0\)

\(\Leftrightarrow\left(x+y\right)^2+6\left(x+y\right)+9=1-y^2\)

\(\left(x+y+3\right)^2=1-y^2\)

Do \(VP=1-y^2\le1\forall x\) \(\Rightarrow VT=\left(x+y+3\right)^2\le1\)

\(\Leftrightarrow-1\le x+y+3\le1\)

\(\Leftrightarrow-1+2013\le x+y+3+2013\le1+2013\)

\(\Leftrightarrow2012\le x+y+2016\le2014\) hay \(2012\le B\le2014\)

B đạt MIN là 2012 \(\Leftrightarrow\hept{\begin{cases}y=0\\x+y+3=-1\end{cases}\Rightarrow\hept{\begin{cases}y=0\\x=-4\end{cases}}}\)

B đạt MAX là 2014 \(\Leftrightarrow\hept{\begin{cases}y=0\\x+y+3=1\end{cases}\Leftrightarrow\hept{\begin{cases}y=0\\x=-2\end{cases}}}\)

\(x^2+2xy+6x+6y+2y^2+8=0\\ \Leftrightarrow\left(x+y\right)^2+6\left(x+y\right)+y^2=-8\)

Ta có \(y^2\ge0\Leftrightarrow\left(x+y\right)^2+6\left(x+y\right)\le-8\)

\(\Leftrightarrow\left(x+y\right)^2+6\left(x+y\right)+9\le1\\ \Leftrightarrow\left(x+y+3\right)^2\le1\\ \Leftrightarrow\left|x+y+3\right|\le1\\ \Leftrightarrow-1\le x+y+3\le1\\ \Leftrightarrow2012\le B\le2014\)

\(B_{min}=2012\Leftrightarrow\left\{{}\begin{matrix}x+y+2016=2012\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=0\end{matrix}\right.\)

\(B_{max}=2014\Leftrightarrow\left\{{}\begin{matrix}x+y+2016=2014\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)

đề bài sai r bn ơi phải là +10 chứ ko phải +8 đâu nhá

\(H=x^2+2xy+y^2+2x+2y+x^2+4x+2019=\left(x+y\right)^2+2\left(x+y\right)+\left(x+2\right)^2+2015\)

\(=\left(x+y+1\right)^2+\left(x+2\right)^2+2014\ge2014\)

Dấu "=" xảy ra \(\Leftrightarrow\)\(x=-2;y=1\)

\(I=\left(1-x\right)^2+\left(-2-y\right)^2+\left(x+y\right)^2\ge\frac{\left(1-x-2-y+x+y\right)^2}{3}=\frac{1}{3}\)

Dấu "=" xảy ra \(\Leftrightarrow\)\(1-x=-2-y=x+y\)\(\Leftrightarrow\)\(x=\frac{4}{3};y=\frac{-5}{3}\)