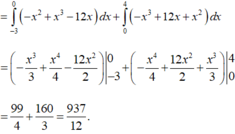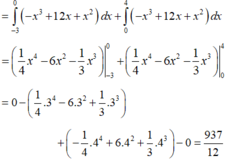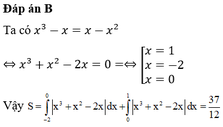tính diện tích S của hình phẳng (H) giới hạn bởi đường cong y= -x3+12x và y=-x2

Những câu hỏi liên quan
Tính diện tích S của hình phẳng (H) giới hạn bởi đường cong
y
-
x
3
+
12
x
và
y
-
x
2
A. S 343/12 B. S 793/4 C. S 397/4 D. S 937/12
Đọc tiếp
Tính diện tích S của hình phẳng (H) giới hạn bởi đường cong y = - x 3 + 12 x và y = - x 2
A. S = 343/12
B. S = 793/4
C. S = 397/4
D. S = 937/12
Hoành độ giao điểm của hai đường cong là nghiệm của phương trình
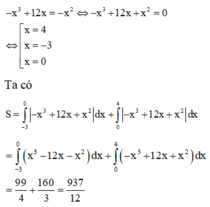
Đáp án D
Đúng 0
Bình luận (0)
Tính diện tích S của hình phẳng (H) giới hạn bởi đường cong y = - x 3 + 12 x v à y = - x 2
A. S=343/12
B. S=793/4
C. S=397/4
D. S=937/12
Tính diện tích S của hình phẳng (H) giới hạn bởi các đường cong
y
−
x
3
+
12
x
và
y
−
x
2
A.
S
937
12
B.
S
343
12
C.
S
793
4
D.
S...
Đọc tiếp
Tính diện tích S của hình phẳng (H) giới hạn bởi các đường cong y = − x 3 + 12 x và y = − x 2
A. S = 937 12
B. S = 343 12
C. S = 793 4
D. S = 397 4
Chọn A.
Phương pháp
Công thức tính diện tích hình phẳng được giới hạn bởi các đường thẳng

Phương trình hoành độ giao điểm của hai đồ thị hàm số đề bài cho là:

Đúng 0
Bình luận (0)
Tính diện tích S của hình phẳng (H) giới hạn bởi các đường cong
y
-
x
3
+
12
x
và
y
-
x
2
Đọc tiếp
Tính diện tích S của hình phẳng (H) giới hạn bởi các đường cong y = - x 3 + 12 x và y = - x 2
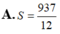
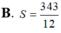
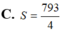
![]()
Diện tích S của hình phẳng (H) giới hạn bởi hai đường cong
y
−
x
3
+
12
x
v
à
y
−
x
2
là A.
S
397
4
B.
S
937
12
C.
S
343
12...
Đọc tiếp
Diện tích S của hình phẳng (H) giới hạn bởi hai đường cong y = − x 3 + 12 x v à y = − x 2 là
A. S = 397 4
B. S = 937 12
C. S = 343 12
D. S = 793 4
Chọn B.
Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số

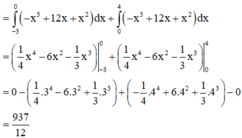
Đúng 0
Bình luận (0)
Diện tích S của hình phẳng (H) giới hạn bởi hai đường cong
y
-
x
3
+
12
x
v
à
y
-
x
2
là:
Đọc tiếp
Diện tích S của hình phẳng (H) giới hạn bởi hai đường cong y = - x 3 + 12 x v à y = - x 2 là:
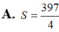
![]()
![]()
![]()
Tính diện tích S của hình phẳng giới hạn bởi hai đường cong y = x 3 - x v à y = x - x 2
A. S= 12/37
B. S= 37/12
C. S= 9/4
D. S= 19/6
Tính diện tích S của hình phẳng giới hạn bởi hai đường cong y = x 3 - x v à y = x - x 2
A. S= 12/37
B. S= 37/12
C. S= 9/4
D. S= 19/6
Cho hình (H) là hình phẳng giới hạn bởi parabol
y
x
2
-
4
x
+
4
, đường cong
y
x
3
và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H) A.
S
11
2
B.
S
7
2
C.
S...
Đọc tiếp
Cho hình (H) là hình phẳng giới hạn bởi parabol y = x 2 - 4 x + 4 , đường cong y = x 3 và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H)
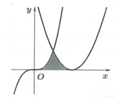
A. S = 11 2
B. S = 7 2
C. S = 20 3
D. S = - 11 2
Hoành độ giao điểm của (C) và (P) là nghiệm phương trình: ![]()
Hoành độ giao điểm của (P) và Ox là nghiệm phương trình:
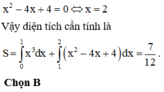
Đúng 0
Bình luận (0)
Cho hình (H) là hình phẳng giới hạn bởi parabol
y
x
2
-
4
x
+
4
đường cong
y
x
3
và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H). A.
S
11
2
B.
S
7
12
C.
S...
Đọc tiếp
Cho hình (H) là hình phẳng giới hạn bởi parabol y = x 2 - 4 x + 4 đường cong y = x 3 và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H).
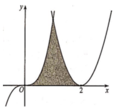
A. S = 11 2
B. S = 7 12
C. S = 20 3
D. S = - 11 2