Chọn B.
Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số

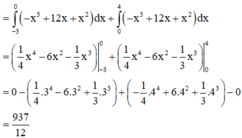
Chọn B.
Phương pháp:
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số

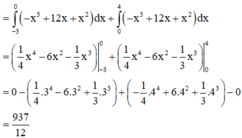
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Tính diện tích S của hình phẳng giới hạn bởi hai đường cong y = x 3 - x v à y = x - x 2
A. S= 12/37
B. S= 37/12
C. S= 9/4
D. S= 19/6
Tính diện tích S của hình phẳng giới hạn bởi hai đường cong y = x 3 - x v à y = x - x 2
A. S= 12/37
B. S= 37/12
C. S= 9/4
D. S= 19/6
Cho hình phẳng (H) giới hạn bởi đường cong có phương trình y = x 2 - 4 x + 3 và đường thẳng y = x + 3 (phần đô đậm trong hình vẽ). Tính diện tích S của hình phẳng (H).
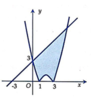
A. S = 47 2
B. S = 39 2
C. S = 169 6
D. S = 109 6
Diện tích S của hình phẳng giới hạn bởi đồ thị hàm số y = x 3 - 4 x , trục hoành và hai đường thẳng x= -2, x=4 là
A. S =44
B. S =8.
C. S =22
D. S=36
Cho hình phẳng (H) giới hạn bởi các đường y = x − 2 ln x + 1 , hai trục tọa độ. Diện tích S của hình phẳng (H) là
A. S = 3 − 2 ln 3.
B. S = 12 − 9 ln 3.
C. S = 4 − 9 2 ln 3.
D. S = 9 2 ln 3 − 4.
Cho hình (H) là hình phẳng giới hạn bởi parabol y = x 2 - 4 x + 4 , đường cong y = x 3 và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H)
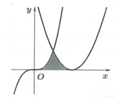
A. S = 11 2
B. S = 7 2
C. S = 20 3
D. S = - 11 2
Cho hình (H) là hình phẳng giới hạn bởi parabol y = x 2 - 4 x + 4 đường cong y = x 3 và trục hoành (phần tô đậm trong hình vẽ). Tính diện tích S của hình (H).
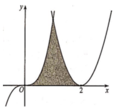
A. S = 11 2
B. S = 7 12
C. S = 20 3
D. S = - 11 2
Hình phẳng được giới hạn bởi các đường y = 4 − x 2 , y = 2 , y = x có diện tích là S = a + b π . Chọn kết quả đúng.
A. a > 1 , b > 1
B. a + b < 1
C. a + 2 b = 3
D. a 2 + 4 b 2 ≥ 5