Nếu \(\Delta ABC=\Delta A'B'C'\) và\(\Delta A'B'C'=\Delta A''B''C''\) thì có \(\Delta ABC=\Delta A''B''C''\) hay không?

Những câu hỏi liên quan
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) có đồng dạng với tam giác \(ABC\) không? Tỉ số đồng dạng là bao nhiêu?
b) Cho tam giác \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng \(k\) thì \(\Delta ABC\backsim\Delta A'B'C'\) theo tỉ số nào?
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).
Đúng 1
Bình luận (0)
1. Cho Delta ABC và Delta DEF có widehat{A}widehat{D}90o. Hãy Bổ sung các yếu tố về góc và cạnh để hai tam giác đó bằng nhau.
2. Cho Delta ABC và Delta ABC đồng dạng với nhau theo ti số k. Gọi AH, AH lần lượt là đường cao củaDelta ABC vàDelta ABC
Cmr: a) Delta ABHsimDelta ABH
b) dfrac{AH}{AH}k
c) dfrac{Delta ABC}{Delta ABC}k
Đọc tiếp
1. Cho \(\Delta ABC\) và \(\Delta DEF\) có \(\widehat{A}=\widehat{D}=90\)o. Hãy Bổ sung các yếu tố về góc và cạnh để hai tam giác đó bằng nhau.
2. Cho \(\Delta ABC\) và \(\Delta A'B'C'\) đồng dạng với nhau theo ti số k. Gọi AH, A'H' lần lượt là đường cao của\(\Delta ABC\) và\(\Delta A'B'C'\)
Cmr: a) \(\Delta ABH\sim\Delta A'B'H'\)
b) \(\dfrac{AH}{A'H'}=k\)
c) \(\dfrac{\Delta ABC}{\Delta A'B'C'}=k\)
Bài 1:
Để ΔABC=ΔDEF thì AB=EF; AC=DF
hoặc cũng có thể là BC=EF và \(\widehat{B}=\widehat{E}\)
Bài 2:
a: Xét ΔABH vuông tại H và ΔA'B'H' vuông tại H' có
\(\widehat{B}=\widehat{B'}\)
Do đó: ΔABH\(\sim\)ΔA'B'H'
b: AH/A'H'=AB/A'B'=k
Đúng 0
Bình luận (0)
Cho Delta ABC đồng dạng với Delta ABC theo hệ số tỉ lệ k_1 4, Delta ABC đồng dạng với Delta ABC theo hệ số tỉ lệ k_2 1/3. Hỏi Delta ABC đồng dạng với Delta ABC theo hệ số tỉ lệ nào ?
Đọc tiếp
Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo hệ số tỉ lệ k\(_1\) = 4, \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo hệ số tỉ lệ k\(_2\) = 1/3. Hỏi \(\Delta A'B'C'\) đồng dạng với \(\Delta A''B''C''\) theo hệ số tỉ lệ nào ?
\(\Delta A'B'C'\)đồng dạng \(\Delta ABC\)theo tỉ số đồng dạng \(\frac{3}{14}\); \(\Delta ABC\)đồng dạng \(\Delta A"B"C"\)theo tỉ số đồng dạng \(\frac{5}{7}\).\(\Delta A'B'C'\)đồng dạng \(\Delta A"B"C"\)theo tỉ số nào ?
Ta có
\(\Delta A'B'C'~\Delta A"B"C"\)theo tỉ số đồng dạng \(k_1\Rightarrow A'B'=k_1A"B"\)
\(\Delta A"B"C"~\Delta A'B'C\)theo tỉ số \(k_2=>A"B"=k_2A"B"=>AB=\frac{A"B"}{k_2}\)
từ đó suy ra
\(\frac{A'B'}{AB}=\frac{k_1A"B"}{\frac{A"B"}{k_2}}=k_1k_2\Leftrightarrow\Delta A'B'C~\Delta ABC\)theo tỉ số \(k_1k_2\)
cho \(\Delta ABC=\Delta A'B'C'\) Biết \(\widehat{A}\): \(\widehat{B}\) : \(\widehat{C}\) bằng 3 : 4 : 5. Tính các góc của \(\Delta A'B'C'\)
Quan sát Hình 12.
a) Chứng minh \(\Delta ABC\backsim\Delta A'B'C'\).
b) Tính độ dài cạnh \(B'C'\).
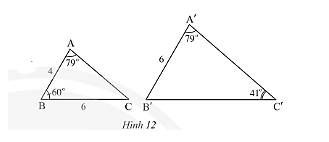
a) Xét tam giác \(A'B'C'\) ta có:
\(\widehat {A'} + \widehat {B'} + \widehat {C'} = 180^\circ \)
Thay số: \(79^\circ + \widehat {B'} + 41^\circ = 180^\circ \)
\( \Rightarrow \widehat {B'} = 180^\circ - 79^\circ - 41^\circ = 60^\circ \)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) ta có:
\(\widehat A = \widehat {A'} = 79^\circ \) (giả thuyết)
\(\widehat B = \widehat {B'} = 60^\circ \) (chứng minh trên)
Do đó, \(\Delta ABC\backsim\Delta A'B'C'\) (g.g)
b) Vì \(\Delta ABC\backsim\Delta A'B'C'\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (các cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{4}{6} = \frac{6}{{B'C'}} \Rightarrow B'C' = \frac{{6.6}}{4} = 9\)
Vậy \(B'C' = 9\).
Đúng 0
Bình luận (0)
a) Trong Hình 11, cho biết Delta ABCbacksimDelta ABC. Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.b) Trong Hình 12, cho biết Delta DEFbacksimDelta DEF. Tính số đo widehat {D} và widehat F.c) Trong Hình 12, cho biết Delta MNPbacksimDelta MNP. Tính độ dài các đoạn thẳng MN và MP.
Đọc tiếp
a) Trong Hình 11, cho biết \(\Delta ABC\backsim\Delta A'B'C'\). Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

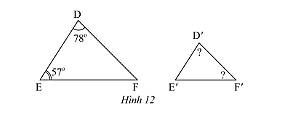
b) Trong Hình 12, cho biết \(\Delta DEF\backsim\Delta D'E'F'\). Tính số đo \(\widehat {D'}\) và \(\widehat F\).
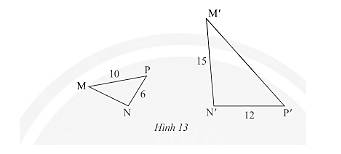
c) Trong Hình 12, cho biết \(\Delta MNP\backsim\Delta M'N'P'\). Tính độ dài các đoạn thẳng \(MN\) và \(MP'\).
a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).
Đúng 0
Bình luận (0)
Nếu \(\Delta ABCđồngdạng\Delta A'B'C'\)theo tỉ số \(k_1=2\) và \(\Delta A'B'C'đồngdạng\Delta A''B''C''\) theo tỉ số \(k_2=\frac{1}{6}\)thì \(\Delta ABCđồngdạng\Delta A''B''C''\)theo tỉ số nào?
cho tam giac ABC va tam giac A'B'C' có AB=A'B', BC=B'C' , \(\widehat{B}+\widehat{B'}=180^0\) Chứng minh \(S_{\Delta ABC}=S_{\Delta A'B'C'}\)













