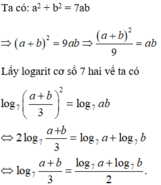Cắp số (x,y) nào thỏa mãnmãn đẳng thức sau 3^2x+1.7^y=9.21^x

Những câu hỏi liên quan
Các số thực x, y thỏa mãn đẳng thức x(3 + 5i) - y(1 + 2i) = 9 + 16i . Giá trị biểu thức T = |x - y| là
A. 0
B. 1
C. 3
D. 5
Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
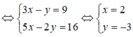
Vậy: T = |x - y| = 5
Đúng 0
Bình luận (0)
Những số nào trong các số -4, -3, -2, -1, 0, 1, 2, 3, 4 là giá trị của số nguyên x thỏa mãn đẳng thức : x . (4 + x) = -3 ?
Ta co:
x.(4+ x) = -3
=> x.4+x.x = -3
=> 2.x(2+1) = -3
=> 2.x.3 =-3
=> 2.x =-3:3
=>2.x =-1
=>x =-1:2
Vay x = -1:2
Đúng 0
Bình luận (0)
tìm các số nguyên x , y thỏa mãn đẳng thức :
\([(x-y)^2+2(xy+y^2-4y)]\)=xy+y2-4y
Cho hai số dương a, b thỏa mãn
a
2
+
b
2
7
a
b
.
Đẳng thức nào sau đây đúng? A.
log
7
a
+
b
2
log
7
a
+
log
7...
Đọc tiếp
Cho hai số dương a, b thỏa mãn a 2 + b 2 = 7 a b . Đẳng thức nào sau đây đúng?
A. log 7 a + b 2 = log 7 a + log 7 b 2
B. log 7 a + b 3 = log 7 a + log 7 b 2
C. log 7 a + b 3 = log 7 a + log 7 b 3
D. log 7 a + b 7 = log 7 a + log 7 b 7
Chứng minh rằng ko tồn tại số hữu tỉ x và y trái dấu và thỏa mãn đẳng thức 1/x+y=1/x + 1/y
\(\frac{1}{x+y}=\frac{1}{x}+\frac{1}{y}\Leftrightarrow\frac{1}{x+y}=\frac{x+y}{xy}\Leftrightarrow xy=\left(x+y\right)^2.\)
mà (x + y)2 >=0 với mọi x;y => xy >= 0. => x;y không thể trái dấu. đpcm
Đúng 0
Bình luận (0)
Cap so (x;y) nao thoa man dang thuc sau: 3^2x+1.7^y=9.21^x
Cac ban giup mk voi!!! Mai phai nop oi!!!!!!!!
Cho các số x,y thỏa mãn đẳng thức 8x2+y2+1/4x2=4.tìm giá trị lớn nhất, nhỉ nhất của P=xy
Tìm các số x, y, z thỏa mãn đẳng thức: \((2x-y)^2+(y-2)^2+\sqrt{(x+y+z)^2}\)\(=0\)
Ta có: \(\left(2x-y\right)^2\ge0\); \(\left(y-2\right)^2\ge0\); \(\sqrt{\left(x+y+z\right)^2}=\left|x+y+z\right|\ge0\)
\(\Rightarrow\left\{{}\begin{matrix}2x-y=0\\y-2=0\\x+y+z=0\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}x=?\\y=?\\z=?\end{matrix}\right.\)
Bạn tự giải :D
Đúng 0
Bình luận (0)
Có hay không số nguyên x thỏa mãn đẳng thức sau:
\(3x^5-x^3+6x^2-18x\text{=}213\)
Ta có: \(3x^5-x^3+6x^2-18x=213\)
\(\Rightarrow x^5-\frac{x^3}{3}+2x^2-6x=71\)
Vì x nguyên nên\(x^5,2x^2,6x\in Z\Rightarrow\frac{x^3}{3}\inℤ\)
\(\Rightarrow x^3⋮3\Rightarrow x⋮3\)(vì 3 là số nguyên tố)
Đặt x = 3k\(\Rightarrow\frac{x^3}{3}=\frac{\left(3k\right)^3}{3}=\frac{27k^3}{3}=9k^3⋮3\)
\(\Rightarrow x^5-\frac{x^3}{3}+2x^2-6x⋮3\)(vì x chia hết cho 3)
.Mà 71 chia 3 dư 2 nên không có số nguyên x thỏa mãn.
Giả sử tồn tại số nguyên x thỏa mãn đề.
Ta có : \(3x^5-x^3+6x^2-18x=213\)
Do : \(213⋮3,3x^5⋮3,6x^2⋮3,18x⋮3\)
\(\Rightarrow x^3⋮3\Rightarrow x⋮3\Rightarrow x^3⋮9\)
Lại có : \(3x^5⋮9,6x^2⋮9,18x⋮9\)
Nên : \(213⋮9\), Mặt khác \(213⋮̸9\)
Do đó không tồn tại số nguyên x thỏa mãn đề.
Giả sử tồn tại số nguyên x thỏa mãn đề bài
\(3x^5-x^3+6x^2-18x=213\)
Có: \(213⋮3;3x^5⋮3;6x^2⋮3;18x⋮3\)
\(\Rightarrow x^3⋮3\Rightarrow x⋮3\Rightarrow x^3⋮9\)
Lại có: \(3x^5⋮9,6x^2⋮9;18x⋮9\)
Mà \(3x^5-x^3+6x^2-18x=213\Rightarrow213⋮9\)
Mặt khác \(213⋮̸9\)
=> PT vô nghiệm