cho tam giác ABC có AB nhỏ hơn AC. qua trung điểm cạnh BC kẻ đường thẳng vuông góc với tia phan giác của góc A cắt AB,AC lần lượt owr M,N
a) CM: BM=CN
b) AM,BM theo AC=b, AC=c
Những câu hỏi liên quan
CHO TAM GIÁC ABC, AB< AC . QUA TRUNG ĐIỂM D CỦA CẠNH BC KẺ ĐƯỜNG VUÔNG GÓC VỚI TIA PHÂN GIÁC CỦA GÓC A CẮT AB VÀ AC LẦN LƯỢT TẠI M VÀ N
Chứng Minh BM=CN
TÍNH AM , BM THEO AC=b , AB= c
http://olm.vn/hoi-dap/question/432504.html
Đúng 0
Bình luận (0)
1) Cho tam giác ABC ,AB<AC. Qua trung điểm D của BC vẽ đường thẳng vuông góc với tia phân giác góc A cắt AB,AC theo thứ tự từ M,N
a. CM: BM = CN
b. Tính: AM,BM theo AC=b, AB=c
Từ trung điểm D của cạnh BC của tam gíac ABC người ta kẻ đường vuông góc với đường pân giác trong của góc A. Đường thẳng này cắt đường thẳng AB và AC lần lượt ở M và N. Chứng minh
a) BM=CM
b) Tính AM và BM theo AC=b, AB=c
Cho tam giác ABC có AB < AC. Qua trung điểm D của BC vẽ đường thẳng vuông góc với tia phân giác của góc A, cắt các cạnh AB, AC theo thứ tự tại M,N.
a) CMR :BM=CN
b)Tính BM, AM theo AC=b, AB=c.
cho tam giác ABC có góc A 45 độ , cạnh AB cạnh AC gọi I là trung điểm cạnh AC , qua I kẻ đường thẳng vuông góc với cạnh AC , cắt đường thảng BC ở M . Trên tia đôi tia AM lấy N sao cho AN BM a) góc AMC góc BACb ) tam giác ABM tam giác CANc ) tam giác MNC vuông cân ở C
Đọc tiếp
cho tam giác ABC có góc A = 45 độ , cạnh AB = cạnh AC gọi I là trung điểm cạnh AC , qua I kẻ đường thẳng vuông góc với cạnh AC , cắt đường thảng BC ở M . Trên tia đôi tia AM lấy N sao cho AN = BM
a) góc AMC = góc BAC
b ) tam giác ABM = tam giác CAN
c ) tam giác MNC vuông cân ở C
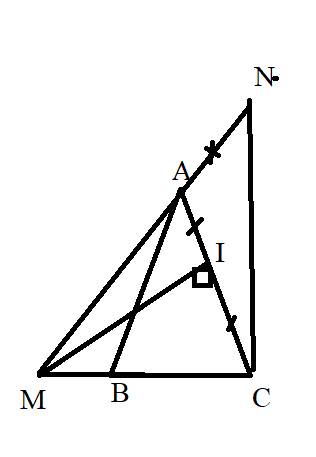
a: Xét ΔMAC có
MI là đường cao
MI là đường trung tuyến
Do đó: ΔMAC cân tại M
=>\(\widehat{AMC}=180^0-2\cdot\widehat{ACM}=180^0-2\cdot\widehat{ACB}\left(1\right)\)
ΔABC cân tại A
=>\(\widehat{BAC}=180^0-2\cdot\widehat{ACB}\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{AMC}=\widehat{BAC}\)
b:
ΔABC cân tại A
=>\(\widehat{ABC}=\widehat{ACB}\)
ΔMAC cân tại M
=>\(\widehat{MAC}=\widehat{MCA}=\widehat{ACB}\)
\(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{ABM}=180^0-\widehat{ABC}=180^0-\widehat{ACB}\left(3\right)\)
\(\widehat{CAN}+\widehat{CAM}=180^0\)(hai góc kề bù)
=>\(\widehat{CAN}+\widehat{ACB}=180^0\)
=>\(\widehat{CAN}=180^0-\widehat{ACB}\left(4\right)\)
Từ (3) và (4) suy ra \(\widehat{ABM}=\widehat{CAN}\)
Xét ΔABM và ΔCAN có
AB=CA
\(\widehat{ABM}=\widehat{CAN}\)
BM=AN
Do đó;ΔABM=ΔCAN
c: ΔABM=ΔCAN
=>NC=MA
mà MA=MC
nên NC=MC
\(\widehat{AMC}=\widehat{BAC}\)
mà \(\widehat{BAC}=45^0\)
nên \(\widehat{AMC}=45^0\)
Xét ΔCMN có CM=CN và \(\widehat{CMN}=45^0\)
nên ΔCMN vuông cân tại C
Đúng 1
Bình luận (0)
Cho tam giác ABC có góc A=45°, AB=AC. Từ trung điểm I của cạnh AC, kẻ đường vuông góc với AC cắt đường thẳng BC ở M. Trên tia đối của tia AM lấy điểm N sao cho AN=BM
a) góc AMC = góc ABC
b) tam giác ABM = tam giác CAM
c) tam giác MNC vuông cân ở C
Cho tam giác ABC ( AB<AC ), Ax là tia phân giác trong của góc A, D là trung điểm của BC. Qua D kẻ đường thẳng vuông góc với Ax, cắt đường thẳng AB và AC lần lượt tại M và N.
a) Chứng minh góc AMN = góc ANM
b) Chứng minh BM = CN
c) Biết AB = 5cm; AC= 7cm. Tính BM?
Cho tam giác ABC ( AB<AC ), Ax là tia phân giác trong của góc A, D là trung điểm của BC. Qua D kẻ đường thẳng vuông góc với Ax, cắt đường thẳng AB và AC lần lượt tại M và N.
a) Chứng minh góc AMN = góc ANM
b) Chứng minh BM = CN
c) Biết AB = 5cm; AC= 7cm. Tính BM?
cho tam giác ABC gọi D là trung điểm của BC. qua D vẽ đường thẳng vuông góc với đường phân giác của A cắt các đường thẳng AB;AC lần lượt tại M;N.
a, chứng minh BM=CN.
b, tính AM;AN theo cạnh AB=c; AC=b
a) tam giác ADM = tam giác ADN (cạnh góc vuông _ góc nhọn)
(AD chung ; ADM^ = ADN^ = 90o; BAD^ = NAD^)
=> DM=DN (2 cạnh t/ứng)
Tam giác BDM = tam giác CDN (c.g.c)
(DB = DC ; BDM^ = CDN^ (đđ); DM = DN)
=> BM = CN (2 cạnh t/ứng)
b) AM = c+ BM
AN = b- NC
(hình như câu b là vậy ^^!)
Đúng 0
Bình luận (0)
