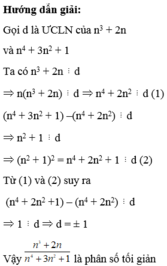Gọi ƯCLN_{(n+2018;n+2019)} = a

Có n+2018 chia hết cho a

và  n+2019 chia hết cho a

=> (n+2019)-(n+2018) chia hết cho a

=> 1 chia hết cho a 

=> a = 1

ƯCLN_{(n+2018;n+2019)} = 1

=> \(\dfrac{n+2018}{n+2019}\) là phân số tối giản

Mình đưa ví dụ nhé:

       n= 1

=>   n+2018/n2019  = 2019/2020

 Bạn thấy đó 2018/ 2019 là phân số tối giản nếu cùng cộng cả tử và mẫu với bao nhiêu đi nữa thì nó cung sẽ luôn tối giản.

    ví dụ như; n+2/n+3

     n=6 

=> 8/9

Đặt \(\left(2n+2018,2n+2019\right)=d\)

\(\Leftrightarrow\hept{\begin{cases}\left(2n+2019\right)⋮d\\\left(2n+2018\right)⋮d\end{cases}}\)

\(\Leftrightarrow\left[\left(2n+2019\right)-\left(2n+2018\right)\right]⋮d\)

\(\Leftrightarrow\left[2n+2019-2n-2018\right]⋮d\)

\(\Leftrightarrow1⋮d\Leftrightarrow d=1\)

Vậy \(\left(2n+2018,2n+2019\right)=1\)hay \(\frac{2n+2018}{2n+2019}\) là phân số tối giản

Gọi d là UCLN của 2n+2018 và 2n+2019

=) 2n+2018 chia hết cho d

=) 2n+2019 chia hết cho d

=) 2n+2019-2n-2018 chia hết cho d

Hay 1 chia hết cho d

=) d=+-1

=) \(\frac{2n+2018}{2n+2019}\)tối giản n thuộc N*

cảm ơn nhiều nhé!

Câu 1

a) A=2018!.(2019 - 1 -2018)

=2018!.0

= 0

vậy A= 0

b)\(B=\left(1-\frac{1}{9}+1-\frac{2}{10}+1+\frac{3}{11}+...+1-\frac{150}{158}\right):\left(\frac{1}{4}.\left(\frac{1}{9}+\frac{1}{10}+\frac{1}{11}+...+\frac{1}{158}\right)\right)\)

\(=\left(\frac{8}{9}+\frac{8}{10}+...+\frac{8}{158}\right):\left(\frac{1}{4}\left(\frac{1}{9}+\frac{1}{10}+...+\frac{1}{158}\right)\right)\)

\(=8.\left(\frac{1}{9}+\frac{1}{10}+...+\frac{1}{158}\right):\left(\frac{1}{4}\left(\frac{1}{9}+\frac{1}{10}+...+\frac{1}{158}\right)\right)\)

\(=8:\frac{1}{4}\)

=32

Vậy B= 32

Đặt \(\left(2n+2018,2n+2019\right)=d\)

\(\Rightarrow\hept{\begin{cases}\left(2n+2018\right)⋮d\\\left(2n+2019\right)⋮d\end{cases}}\)

\(\Leftrightarrow\left[\left(2n+2019\right)-\left(2n+2018\right)\right]⋮d\)

\(\Leftrightarrow\left[2n+2019-2n-2018\right]⋮d\)

\(\Leftrightarrow1⋮d\)\(\Leftrightarrow d=1\)

Vậy \(\left(2n+2018,2n+2019\right)=1\)hay \(\frac{2n+2018}{2n+2019}\) tối giản.

Gọi ƯCLN( 2n + 2018 ; 2n + 2019 ) là d                                                                                                                                                              =>2n + 2018 chia hết d                                                                                                                                                                                        =>2n + 2019 chia hết d                                                                                                                                                                                                ->(2n + 2019) - (2n + 2018) chia hết d                                                                                                                                                                        =>1 chia hết cho d                                                                                                                                                                                               =>d E Ư(1)={1}                                                                                                                                                                                              Vậy vs moị STN n thì phân số trên đều tối giản

Gọi d=(2n+2018,2n+2019)

=>d chia hêt cho2n+2018 và 2n+2019

=>(2n+2019)-(2n+2018) chia hêt cho d

=>1 chia hêt cho d

=>d=1

Vậy=>ĐPCM

Ta có ps tối giản khi bỏ n là : 2017/2018 

Vì n là số giống nhau nên khi cộng vs phân số tối giản thì sau khi cộng thì vx là 1 ps tối giản

Ta có ví dụ sau:

n = 2 

2 + 2017/ 2 + 2018

= 2019/2020 Là phân số tối giản

Ta sẽ thử lại 1 lần nữa:

n = 5

5 + 2017/ 5 + 2018

= 2022/2023 

Vậy phân số n+2017/n+2018 là phân số tối giản

\(\text{Gọi ƯCLN của n + 2017; n + 2018 là a }\)
\(\Rightarrow\hept{\begin{cases}n+2017⋮a\\n+2018⋮a\end{cases}}\)

\(\Rightarrow\left(n+2017\right)-\left(n+2018\right)⋮a\)

\(n+2017-n-2018⋮a\)

\(-1⋮a\)

\(\Rightarrow a\in\text{Ư}\left(-1\right)=\left\{\pm1\right\}\)
\(\text{Mà a là ƯCLN của n + 2017; n + 2018 }\)

\(\Rightarrow a=1\)

\(\Rightarrow\frac{n+2017}{n+2018}\text{ tối giản}\)

Gọi ƯCLN(n+2017;n+2018) là d

=>\(\hept{\begin{cases}n+2017\\n+2018\end{cases}}\)\(⋮\)d =>(n+2017)-(n+2018)\(⋮\)d

=>-1\(⋮\)d

=>1\(⋮\)d

=>d=1

=>đpcm

a: Để A nguyên thì \(n+2\in\left\{1;-1;3;-3\right\}\)

=>\(n\in\left\{-1;-3;1;-5\right\}\)

b: n+6/n+7

Gọi d=ƯCLN(n+6;n+7)

=>n+6-n-7 chiahết cho d

=>-1 chia hết cho d

=>d=1

=>PSTG

Gọi d=ƯCLN(n+1;n)

=>\(\left\{{}\begin{matrix}n+1⋮d\\n⋮d\end{matrix}\right.\)

=>\(n+1-n⋮d\)

=>\(1⋮d\)

=>d=1

=>ƯCLN(n+1;n)=1

=>\(\dfrac{n+1}{n}\) là phân số tối giản