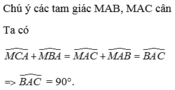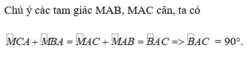Cho Tam giac ABM cân tại M. Trên tia đối của tia MB lấy điểm C sao cho MC=MB. Tính góc BAC

Những câu hỏi liên quan
Cho tam giác MAB cân tại M. Trên tia đối của tia MB lây điểm C sao cho MC = MB. Tính số đo góc BAC.
Cho tam giác MAB cân tại M. Trên tia đối của tia MB lây điểm C sao cho MC = MB. Tính số đo góc BAC.
Cho tam giác ABM cân tại M nội tiếp (O) . Trên tia đối của tia MB lấy C: MC=MB. Nối AC cắt đường tròn tại điểm thứ hai D. Gọi E là điểm đối xứng của D qua A
a) c/m góc BEC=2.góc ACB
b) c/m: CD.CA=BC2 : 2
c) Tia BE và MA cắt nhau tịa F. c/m AE=EF và BF=AC
d) Tìm điều kiện của tam giác ABM để tg MDFE là hình bình hành
Cho tam giác ABM cân tại M nội tiếp (O) . Trên tia đối của tia MB lấy C: MC=MB. Nối AC cắt đường tròn tại điểm thứ hai D. Gọi E là điểm đối xứng của D qua A
a) c/m góc BEC=2.góc ACB
b) c/m: CD.CA=BC2 : 2
c) Tia BE và MA cắt nhau tịa F. c/m AE=EF và BF=AC
d) Tìm điều kiện của tam giác ABM để tg MDFE là hình bình hành
Cho tam giác ABC cân tại A lấy điểm M trên tia đối BC lấy điểm N trên tia đối CB sao cho BM bằng CN a, góc ABM bằng góc CAN b,tam giác AMN cân c,so sánh AM,AC d, trên tia đối của tia MA lấy điểm I sao cho MI bằng AM. Nếu MB bằng BC bằng CN thì AB đi qua trung điểm của IN c,so sánh AM, AC
a: Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
b:
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
c: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}\) nhọn
=>\(\widehat{ABM}=180^0-\widehat{ABC}>90^0\)
Xét ΔABM có \(\widehat{ABM}>90^0\)
mà AM là cạnh đối diện của góc ABM
nên AM là cạnh lớn nhất trong ΔABM
=>AM>AB
mà AB=AC
nên AM>AC
Đúng 0
Bình luận (0)
cho tam giác AMB cân tại M trên tia đối của tia MB lấy điểm C sao cho MB=MC .CMR gốc CAB =90 độ
Cho tam giác MAB cân tại M.Trên tia đối của tia MB lấy điểm C sao cho MB=MC.Tính số đo góc BAC
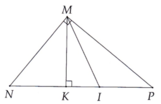
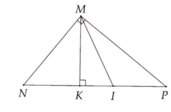
\(\Delta ABM\)cân tại \(M\)
\(=>\hept{\begin{cases}MAB=MBA\\MA=MB< =>MC=MA\end{cases}}\)
\(=>\Delta AMC\)cân tại \(M\)
\(=>MCA=MAC\)
Xét \(\Delta ABM\)có
\(AMB+MAB+MBA=180^0\)
\(=>2MAC+2MAB=180^0\)
\(=>2CAB=180^0\)
\(=>CAB=90^0\)
cho tam giác ABM cân tại A. đường cao AI, lấy điểm D sao cho I là trung điểm AD. Trên tia đối của MB lấy điểm C sao cho MB=MC
a) Chứng minh BC là phân giác góc ABD
b) Gọi K là trung điểm CD. Chứng K,A,M thẳng hàng
c) Giả sử BC= 2AB thì tam giác ABM; tam giác ACM, tam giác ACD là tam giác gì?
A) XÉT \(\Delta BAI\)VÀ \(\Delta BDI\)CÓ
BI LÀ CẠNH CHUNG
\(\widehat{BIA}=\widehat{BID}=90^o\)
\(AI=DI\left(gt\right)\)
=>\(\Delta BAI\)=\(\Delta BDI\)(C-G-C)
=> \(\widehat{ABI}=\widehat{DBI}\)HAY \(\widehat{ABC}=\widehat{DBC}\)
=> BC LÀ PHÂN GIÁC CỦA GÓC\(\widehat{ABD}\)
B) VÌ AI = DI (GT)
=> CI LÀ ĐƯỜNG TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ACD\)
TA CÓ \(BM=CM\left(GT\right)\)
THAY \(BI+MI=CM\)
MÀ BI = MI (GT)
\(\Rightarrow2MI=CM\)
MÀ CI LÀ ĐƯỜNG TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ACD\)
=> M LÀ TRỌNG TÂM CỦA \(\Delta ACD\)
TA CÓ DK = CK (GT)
=> AK LÀ ĐƯỜNG TRUNG TUYẾN THỨ HAI CỦA \(\Delta ACD\)
=> AK BẮT BUỘT ĐI QUA TRỌNG TÂM M
=> A,K,M THẲNG HÀNG
C) THEO GT TA CÓ
\(BC=2AB\)
\(\Leftrightarrow BC=AB+AB\)
\(\Leftrightarrow BC=AB+AM\)( AB = AM )
\(\Leftrightarrow BM+CM=AB+AM\)
\(\Leftrightarrow2CM=2AM\)( BM=CM ; AB=AM)
\(\Leftrightarrow CM=AM\)
=> \(\Delta ACM\)CÂN TẠI M
ACD LÀ TAM GIÁC CÂN
VÌ TRONG TAM GIÁC CÓ HAI ĐƯỜNG TRUNG TUYẾN Ở GÓC ĐÁY = NHAU
=> \(\Delta\)ĐÓ LÀ TAM GIÁC CÂN
cho tam giac ABC vuong tai A. Gọi M là trung điểm của AC; trên tia đối của tia MB lấy điểm D sao cho MD=MB
a; cmr: AD=BC
b; cmr: CD vuông góc với AC
c; đường thẳng B song song với AC cắt DC tại N. cmr : tam giac ABM= tam giac CNM