a: 

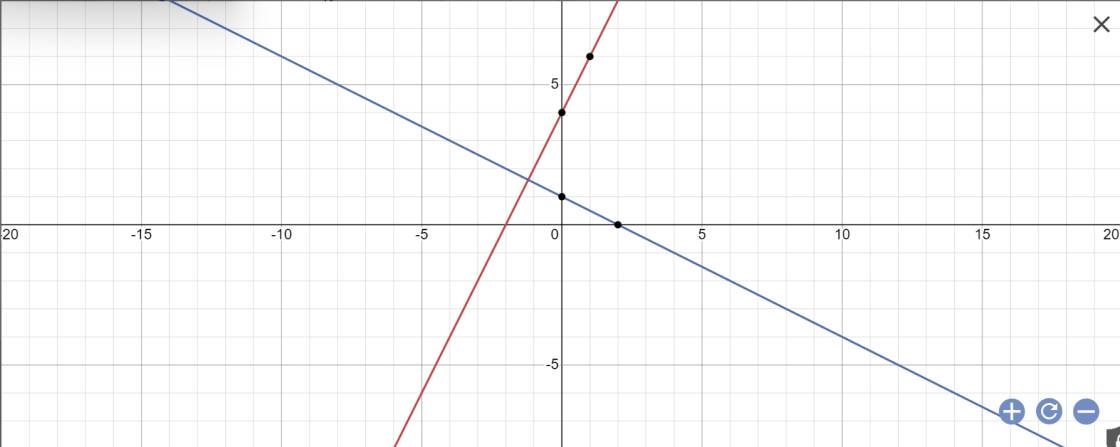
b: Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\2x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=2x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0+4=4\end{matrix}\right.\)

Tọa độ C là:

\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+1=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)

Tọa độ M là:

\(\left\{{}\begin{matrix}2x+4=-\dfrac{1}{2}x+1\\y=2x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{2}x=-3\\y=2x+4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=-3:\dfrac{5}{2}=-3\cdot\dfrac{2}{5}=-\dfrac{6}{5}\\y=2\cdot\dfrac{-6}{5}+4=\dfrac{-12}{5}+4=\dfrac{8}{5}\end{matrix}\right.\)

A(-2;0); C(2;0); M(-1,2;1,6)

\(AC=\sqrt{\left(2+2\right)^2+\left(0-0\right)^2}=\sqrt{4^2}=4\)

\(AM=\sqrt{\left(-1,2+2\right)^2+\left(1,6-0\right)^2}=\dfrac{4\sqrt{5}}{5}\)

\(CM=\sqrt{\left(-1,2-2\right)^2+1,6^2}=\dfrac{8\sqrt{5}}{5}\)

Vì \(MA^2+MC^2=AC^2\)

nên ΔMAC vuông tại M

c: Vì ΔMAC vuông tại M

nên \(S_{MAC}=\dfrac{1}{2}\cdot MA\cdot MC=\dfrac{1}{2}\cdot\dfrac{4\sqrt{5}}{5}\cdot\dfrac{8\sqrt{5}}{5}=\dfrac{2\cdot8}{5}=\dfrac{16}{5}\)

a)(d1) vuông góc với (d2) tại M (vì tích hệ số góc của 2 đường thẳng a

\(\times\)a'=2\(\times\)\(-\dfrac{1}{2}\)=-1

vậy tam giác MAC vuông tại M

b)hoành độ M là nghiệm của phương trình:

2x+4=\(-\dfrac{1}{2}\)x+1

<=>2x+\(\dfrac{1}{2}\)x=1-4

<=>\(\dfrac{5}{2}\)x =-3

<=> x=\(\dfrac{-6}{5}\)

=> Y=2\(\times\)\(\dfrac{-6}{5}\)+4=\(\dfrac{8}{5}\)

AC=4(vẽ sơ đồ là bạn có thể bt đc)

diện tích tam giác AMC là

Samc=\(\dfrac{1}{2}\)\(\times\)AC\(\times\)MH

=\(\dfrac{1}{2}\)\(\times\)4\(\times\)\(\dfrac{8}{5}\)=\(\dfrac{16}{5}\)(đơn vị diện tích)

Vì 2*(-1/2)=-1

nên (d1) vuông góc với (d2)

=>ΔMAC vuông tại M

Câu 2: 

Tọa độ điểm A là:

\(\left\{{}\begin{matrix}y=0\\2x+4=0\end{matrix}\right.\Leftrightarrow A\left(-2;0\right)\)

Tọa độ điểm B là:

\(\left\{{}\begin{matrix}x=0\\y=2\cdot0+4=4\end{matrix}\right.\)

=>B(0;4)

Tọa độ điểm C là:

\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+1=0\end{matrix}\right.\Leftrightarrow C\left(2;0\right)\)

Tọa độ điểm D là:

\(\left\{{}\begin{matrix}x=0\\y=\dfrac{-1}{2}\cdot0+1=1\end{matrix}\right.\Leftrightarrow D\left(0;1\right)\)

Tọa độ điểm M là:

\(\left\{{}\begin{matrix}2x+4=-\dfrac{1}{2}x+1\\y=2x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1,2\\y=1,6\end{matrix}\right.\)

M(-1,2;1,6); A(-2;0); B(0,4); C(2;0); D(0;1)

\(\overrightarrow{MA}=\left(-0.8;-1.6\right)\)

\(\overrightarrow{MC}=\left(3.2;-1.6\right)\)

Vì \(\overrightarrow{MA}\cdot\overrightarrow{MC}=0\)

nên ΔMAC vuông tại M

b: \(MA=\sqrt{\left(-0.8\right)^2+\left(-1.6\right)^2}=\dfrac{4}{5}\sqrt{5}\)

\(MC=\sqrt{3.2^2+1.6^2}=\dfrac{8}{5}\sqrt{5}\)

\(S_{MAC}=\dfrac{4}{5}\sqrt{5}\cdot\dfrac{8}{5}\sqrt{5}:2=3.2\)

a: Đặt (d1): y=ax+b(a<>0)

Vì (d1) vuông góc với (d) nên 3a=-1

=>\(a=-\dfrac{1}{3}\)

Vậy: (d1): \(y=-\dfrac{1}{3}x+b\)

Tọa độ A là:

\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\-\dfrac{1}{3}x=-b\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=0\\\dfrac{x}{3}=b\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3b\\y=0\end{matrix}\right.\)

=>A(3b;0)

Tọa độ B là:

\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{3}\cdot0+b=b\end{matrix}\right.\)

=>B(0;b)

\(AB=2\sqrt{10}\)

=>\(AB^2=40\)

=>\(\left(0-3b\right)^2+\left(b-0\right)^2=40\)

=>\(10b^2=40\)

=>\(b^2=4\)

=>b=2 hoặc b=-2

Vậy: (d1): y=-1/3x+2 hoặc (d1): y=-1/3x-2

b: Đặt (d2): y=ax+b

Vì (d2)//(d) nên \(\left\{{}\begin{matrix}a=3\\b\ne-5\end{matrix}\right.\)

Vậy: (d2): y=3x+b

Tọa độ C là:

\(\left\{{}\begin{matrix}y=0\\3x+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{b}{3}\end{matrix}\right.\)

=>\(C\left(-\dfrac{b}{3};0\right)\)

tọa độ D là:

\(\left\{{}\begin{matrix}x=0\\y=3x+b=3\cdot0+b=b\end{matrix}\right.\)

=>D(0;b)

\(OC=\sqrt{\left(-\dfrac{b}{3}-0\right)^2+\left(0-0\right)^2}=\sqrt{\left(\dfrac{b}{3}\right)^2+0}=\dfrac{\left|b\right|}{3}\)

\(OD=\sqrt{\left(0-0\right)^2+\left(b-0\right)^2}=\sqrt{0^2+b^2}=\left|b\right|\)

Vì Ox\(\perp\)Oy nên OC\(\perp\)OD

=>ΔOCD vuông tại O

=>\(S_{OCD}=\dfrac{1}{2}\cdot OC\cdot OD\)

=>\(S_{OCD}=\dfrac{\dfrac{1}{2}\left|b\right|}{3}\cdot\left|b\right|=\dfrac{1}{2}\cdot\dfrac{b^2}{3}\)

Để \(S_{OCD}=6\) thì \(\dfrac{b^2}{6}=6\)

=>\(b^2=36\)

=>\(b=\pm6\)

Vậy: (d2): y=3x+6 hoặc (d2): y=3x-6

Để ΔOCD cân tại O thì OC=OD

=>\(\dfrac{\left|b\right|}{3}=\left|b\right|\)

=>\(\left|b\right|=0\)

=>b=0

Vậy: (d2): y=3x