đại lượng y có phải là hàm số của đại lượng xkhoong

Những câu hỏi liên quan
Đại lượng x lấy các giá trị là các số tự nhiên. Đại lượng y lấy giá trị là ước của x. Đại lượng y có phải là hàm số của đại lượng x không?
Đại lượng x lấy giá trị là các số tự nhien, đại lượng y lấy giá trị là số dư của phép chia cho 5. Đại lượng y có phải là hàm số của đại lượng x hay không ?
Đại lượng x giá trị là các số thực, đại lượng y lấy giá trị bằng x nếu x>= 0 , bang -x nếu x<0. Đại lượng y có phải là hàm số của đại lượng x ko ? Nếu có hãy viết công thức xác định hàm số này.
Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là số dư phép chia x cho 3. Đại lượng y có phải là hàm số của đại lượng x không?Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là ước của x. Đại lượng y có phải là hàm số của đại lượng x không?CMR: a)Tổng của 1 số hữu tỉ và 1 số vô tỉ là 1 số vô tỉb) Tích của một số hữu tỉ khác 0 với 1 số vô tỉ là 1 số VTc) Thương của 1 số HT với 1 số VT là 1 số VT
Đọc tiếp
Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là số dư phép chia x cho 3. Đại lượng y có phải là hàm số của đại lượng x không?
Đại lượng x lấy các giá trị là các số tự nhiên, đại lượng y lấy giá trị là ước của x. Đại lượng y có phải là hàm số của đại lượng x không?
CMR: a)Tổng của 1 số hữu tỉ và 1 số vô tỉ là 1 số vô tỉ
b) Tích của một số hữu tỉ khác 0 với 1 số vô tỉ là 1 số VT
c) Thương của 1 số HT với 1 số VT là 1 số VT
1.Đại lượng y là hàm số của đại lượng x vì ta có mỗi giá trị của đại lượng x đều có một giá trị tương ứng của đại lượng y . Giá trị tương ứng ấy của đại lượng y là duy nhất.
2. Đại lượng y không phải là hàm số của đại lượng x vì ứng với giá trị x = 5 chẳng hạn ta có hai giá trị của y (ước tự nhiên của 5 là 1 và 5)
3. Dựa vào định nghĩa các phép toán về số hữu tỉ. Chú ý rằng với các số hữu tỉ thì kết quả của các phép toán này là số hữu tỉ. Chẳng hạn câu b). Giả sử tích của số hữu tỉ \(x\ne0\)với số vô tỉ y là số hữu tỉ z. Ta có x.y=z.
Như vậy thì \(y=\frac{z}{x}\). Nhưng z và x \(\left(x\ne0\right)\)là hai số hữu tỉ nên thương của chúng cũng là số hữu tỉ. Suy ra y là số hữu tỉ, trái với đề bài. Vậy tích của một số hữu tỉ khác 0 với một số vô tỉ là một số vô tỉ.
Đúng 0
Bình luận (0)
Đại lượng x lấy giá trị là các số thực, đại lượng y lấy giá trị bằng x nếu x≥0, bằng −x nếu x<0. Đại lượng y có phải là hàm số của đại lượng x không ?
Các giá trị tương ứng của hai đại lượng \(x\) và \(y\) được cho trong bảng sau. Trong mỗi trường hợp, hãy cho biết đại lượng \(y\) có phải là hàm số của đại lượng \(x\) không? Giải thích.
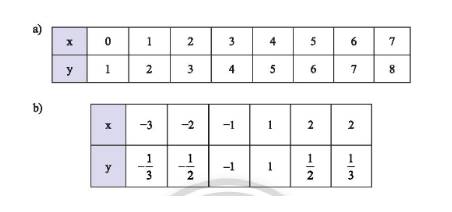
a) Bảng a đại lượng \(y\) là hàm số của đại lượng \(x\) vì với mỗi giá trị của \(x\) ta chỉ nhận được duy nhất một giá trị tương ứng của \(y\).
b) Bảng b đại lượng \(y\) không là hàm số của đại lượng \(x\) vì có những giá trị của \(x\) cho ta hai giá trị \(y\).
Với \(x = 2\) cho ta hai giá trị \(y\) là \(y = \dfrac{1}{2}\) và \(y = \dfrac{1}{3}\).
Đúng 0
Bình luận (0)
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
x
4
4
9
16
y
-2
2
3
4
Đọc tiếp
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
| x | 4 | 4 | 9 | 16 |
| y | -2 | 2 | 3 | 4 |
Trong bảng ta thấy ứng với giá trị x = 4 có hai giá trị khác nhau của y là 2 và -2. Theo định nghĩa thì y không phải là hàm số của đại lượng x.
Đúng 0
Bình luận (0)
Đại lượng y trong bảng nào sau đây không phải là hàm số của đại lượng x tương ứng:
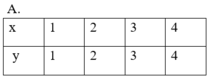
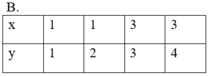
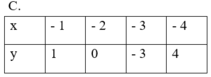
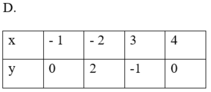
Quan sát bảng ở đáp án B ta thấy, với x = 1 và x = 3 thì tồn tại hai giá trị tương ứng của y. Do đó, đại lượng y ở bảng B không phải là hàm số của đại lượng x
Chọn đáp án B
Đúng 0
Bình luận (0)
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
x
-2
-1
0
1
2
y
1
1
1
1
1
Đọc tiếp
Đại lượng y có phải là hàm số của đại lượng x không, nếu bảng các giá trị tương ứng của chúng là:
| x | -2 | -1 | 0 | 1 | 2 |
| y | 1 | 1 | 1 | 1 | 1 |
Trong bảng ta thấy ứng với mỗi giá trị của x ta luôn xác định được chỉ một giá trị của y. Theo định nghĩa thì y là hàm số của đại lượng x. Ở đây giá trị của y không đổi nên hàm số là hàm hằng.
Đúng 0
Bình luận (0)











