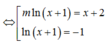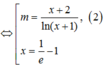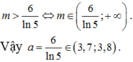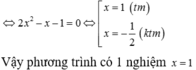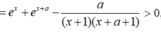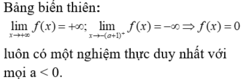Tìm $m$ để phương trình $m\ln (1-x)-\ln x=m$ có nghiệm $x \in (0;1)$.

Những câu hỏi liên quan
Tìm tất cả các giá trị của tham số m để phương trình
ln
(
m
+
ln
(
m
+
x
)
)
x
có 2 nghiệm phân biệt A. m ≥ 0 B. m 1 C. m e D. m ≥ -1
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình ln ( m + ln ( m + x ) ) = x có 2 nghiệm phân biệt
A. m ≥ 0
B. m > 1
C. m < e
D. m ≥ -1
ĐỀ THI HỌC KỲ I Câu 1 : giải phương trình ln (3x2 - 2x +1) ln ( 4x - 1) Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 m sqrt{9^x+1} có đúng 1 nghiệm Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
Đọc tiếp
ĐỀ THI HỌC KỲ I
Câu 1 : giải phương trình ln (3x2 - 2x +1) = ln ( 4x - 1)
Câu 2 : Tìm tập hợp các giá trị của tham số m để phương trình 3x + 3 = m \(\sqrt{9^x+1}\) có đúng 1 nghiệm
Câu 3 : Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số y = -x3 + 3mx + 1 có 2 điểm cực trị A , B sao cho tam giác OAB vuông tại O ( với O là gốc tọa độ )
Cho phương trình
m
.
l
n
2
(
x
+
1
)
-
(
x
+
2
-
m
)
l
n
(
x
+
1
)
-
x
-
2
0
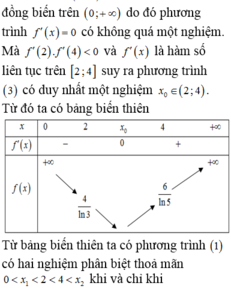
(1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn
0...
Đọc tiếp
Cho phương trình m . l n 2 ( x + 1 ) - ( x + 2 - m ) l n ( x + 1 ) - x - 2 = 0 (1). Tập hợp tất cả các giá trị của tham số m để phương trình (1) có hai nghiệm phân biệt thoả mãn 0 < x 1 < 2 < 4 < x 2 là khoảng . Khi đó a thuộc khoảng
![]()
![]()
![]()
![]()
Tìm số nghiệm của phương trình
ln
(
x
)
+
ln
(
2
x
-
1
)
0
A. 2 B. 4 C. 1 D. 0
Đọc tiếp
Tìm số nghiệm của phương trình ln ( x ) + ln ( 2 x - 1 ) = 0
A. 2
B. 4
C. 1
D. 0
Tập hợp các số thực m để phương trình
ln
x
2
-
m
x
-
2019
ln
x
có nghiệm duy nhất là A.
∅
B.
-
1
C.
0
D.
ℝ...
Đọc tiếp
Tập hợp các số thực m để phương trình ln x 2 - m x - 2019 = ln x có nghiệm duy nhất là
A. ∅
B. - 1
C. 0
D. ℝ
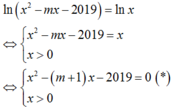
Nhận thấy phương trình (*) có a c < 0 ⇒ * có 2 nghiệm phân biệt, do đó ∀ m ∈ ℝ phương trình (*) luôn có 1 nghiệm thỏa mãn x > 0 .
Chọn D.
Đúng 0
Bình luận (0)
tìm m để bất phương trình sau có nghiệm
\(\begin{cases} (2x+1)[ln(x+1)-lnx]=(2y+1)[ln(y+1)-lny]\\ \sqrt{y-1} -2 \sqrt[4]{(y+1)(x-1)} +m\sqrt{x+1}=0 \end{cases}\)
Có bao nhiêu số nguyên
a
∈
(
-
200
;
200
)
để phương trình
e
x
+
e
x
+
a
ln
(
1
+
x
)
-
ln
(
x
+
a...
Đọc tiếp
Có bao nhiêu số nguyên a ∈ ( - 200 ; 200 ) để phương trình e x + e x + a = ln ( 1 + x ) - ln ( x + a + 1 ) có nghiệm thực duy nhất.
A. 399
B. 199
C. 200
D. 398
Cho hàm số y f(x) liên tục trên
ℝ
và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình
f
(
e
x
)
m
có nghiệm thuộc khoảng (0; ln 3) là: A. (1;3) B.
-
1
3
;
0
C....
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f ( e x ) = m có nghiệm thuộc khoảng (0; ln 3) là:
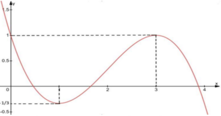
A. (1;3)
B. - 1 3 ; 0
C. - 1 3 ; 1
D. - 1 3 ; 1
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn
Đúng 2
Bình luận (1)