cmr đường thẳng đi qua hình thang cân là trục đối xứng của hình thang cân đó

Những câu hỏi liên quan
Thế nào là hai điểm đối xứng với nhau qua một đường thẳng? Trục đối xứng của hình thang cân là đường thẳng nào?
- Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó.
- Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai đáy của hình thang cân.
Đúng 0
Bình luận (0)
Thế nào là hai điểm đối xứng với nhau qua một đường thẳng ? Trục đối xứng của hình thang cân là đường thẳng nào ?
Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó. Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Đúng 0
Bình luận (0)
Hai điểm gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của đoạn thẳng nối hai điểm đó. Đường thẳng đi qua trung điểm hai đáy của hình thang cân là trục đối xứng của hình thang đó.
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI=AK.
a)CMR: I đối xứng với K qua H.
b)CMR: BIKC là hình thang cân.
c) Gọi giao điểm của BK và IC là G. GH có phảI trục đối xứng của hình thang cân BIKC không? Tại sao?
Cho tam giác ABC cân tại A, đường cao AH. Trên cạnh AB lấy điểm I, trên cạnh AC lấy điểm K sao cho AI=AK.
a)CMR: I đối xứng với K qua H.
b)CMR: BIKC là hình thang cân.
c) Gọi giao điểm của BK và IC là G. GH có phảI trục đối xứng của hình thang cân BIKC không? Tại sao?
b: Xét ΔABC có
\(\dfrac{AI}{AB}=\dfrac{AK}{AC}\)
Do đó: IK//BC
Xét tứ giác BIKC có IK//BC
nên BIKC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BIKC là hình thang cân
Đúng 1
Bình luận (0)
Bài 1: Cho hình thang cân ABCD (BC//AD). Từ B,C kẻ các đường thẳng tương ứng song song với AC,BD cắt nhau tại E. Gọi O là giao điểm của AC,BD. CMR:
a) E và O đối xứng nhau qua BC
b) OE là trục đối xứng của hình thang cân ABCD
Bài 2: Cho đường thẳng d và 2 điểm A,BB nằm khác phía với nhau. Hãy xác định điểm M trên d sao cho |MA-MB| lớn nhất.
đường thẳng,tam giác, tam giác cân, tam giác đều, tứgiác, hình thang, hình thang cân, hình bình hành, hình chữnhật, hình thoi, hình tròn có bao nhiêu trục và tâm đối xứng
Chứng minh rằng giao điểm hai đường chéo hình thang cân nằm trên trục đối xứng của hình thang cân.
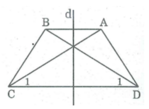
Hình thang cân ABCD có AB // CD
Gọi O là giao điểm của hai đường chéo AC và BD.
Xét ∆ ADC và ∆ BCD:
AD = BC (tính chất hình thang cân)
AC = BD (tính chất hình thang cân)
CD chung
Do đó ∆ ADC= ∆ BCD (c.c.c)
⇒ ∠ D 1 = ∠ C 1
⇒ ∆ OCD cân tại O
⇒ OC = OD nên O nằm trên đường trung trực của CD.
Trục đối xứng hình thang cân là đường thẳng trung trực của hai đáy.
Vậy O thuộc trục đối xứng của hình thang cân.
Đúng 0
Bình luận (0)
Vẽ hình thang cân:
Cho trước ba điểm A, B, C. Dựng đỉnh D của hình thang cân ABCD dựa trên các công cụ đoạn thẳng, đường trung trực và phép biến đổi đối xứng qua trục.

Đặc điểm hình thang cân:
AD // BC, AB = CD
d là đường trung trực BC thì d cũng là đường trung trực cạnh AD
Các bước vẽ hình thang cân:
Sử dụng công cụ tạo điểm mới để tạo ba điểm A, B, C.
Sử dụng công cụ đường trung trực vẽ đường trung trực của cạnh BC
Sử dụng công cụ đối xứng vẽ điểm đối xứng của A qua trục đối xứng
Đúng 0
Bình luận (0)
Chứng minh rằng giao điểm hai đường chéo của hình thang cân nằm trên trục đối xứng của hình thang cân ?
















