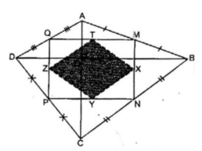
Kẻ đường chéo MP và NQ

Trong  △ MNP ta có:

X là trung điểm của MN

Y là trung điểm của NP

nên XY là đường trung bình của  △ MNP

⇒ XY // MP và XY = 1/2 MP (tính chất đường trung bình của tam giác) (3)

Trong  △ QMP ta có:

T là trung điểm của QM

Z là trung điểm của QP

nên TZ là đường trung bình của  △ QMP

⇒ TZ // MP và TZ = 1/2 MP (tính chất đường trung bình của tam giác) (4)

Từ (3) và (4) suy ra: XY // TZ và XY = TZ nên tứ giác XYZT là hình bình hành.

Trong △ MNQ ta có XT là đường trung bình

⇒ XT = 1/2 QN (tính chất đường trung bình của tam giác)

Tứ giác MNPQ là hình chữ nhật ⇒ MP = NQ

Suy ra: XT = XY. Vậy tứ giác XYZT là hình thoi

S X Y Z T  = 1/2 XZ. TY

mà XZ = MQ = 1/2 BD = 1/2. 8 = 4 (cm);

TY = MN = 1/2 AC = 1/2 .6 =3 (cm)

Vậy : S X Y Z T  = 1/2. 3. 4 = 6( c m 2 )

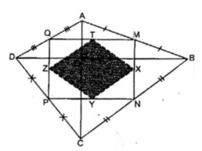
Trong  △ ABD ta có:

M là trung điểm của AB

Q là trung điểm của AD nên MQ là đường trung bình của  △ ABD.

⇒ MQ // BD và MQ = 1/2 BD (tính chất đường trung bình của tam giác) (1)

Trong  △ CBD ta có:

N là trung điểm của BC

P là trung điểm của CD

nên NP là đường trung bình của  △ CBD

⇒ NP // BD và NP = 1/2 BD (tính chất đường trung bình của tam giác) (2)

Từ (1) và (2) suy ra: MQ // NP và MQ = NP nên tứ giác MNPQ là hình bình hành

AC ⊥ BD (gt)

MQ // BD

Suy ra: AC ⊥ MQ

Trong △ ABC có MN là đường trung bình ⇒ MN // AC

Suy ra: MN ⊥ MQ hay (NMQ) = 90 0

Vậy tứ giác MNPQ là hình chữ nhật.

Em tự vẽ hình nhé. Ý sau cô nói rõ yêu cầu hơn là chứng minh hình bình hành MNPQ có chu vi bằng tổng độ dài hai đường chéo của tứ giác ABCD.

Xét tứ giác EFMN có OF = ON; OE = OM nên nó là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường)

Vậy thì MN // EF // AC và MN = EF = AC / 2 (Vì EF là đường trung bình tam giác BAC).

Hoàn toàn tương tự: QP // GH // AC và QP = GH = AC/2.

Vậy MNPQ là hình bình hành (Cặp cạnh đối song song và bằng nhau).

Khi đó ta có:

 \(p_{MNPQ}=PQ+PN+NM+MQ=\left(PQ+MN\right)+\left(MQ+PN\right)=AC+BD.\)

Vậy ta đã chứng minh xong bài toán.

Cô ơi em ko hiểu.Theo em thì ta phải cm MN//=AC và PQ//=AC

* Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC nên MN là đường trung bình của tam giác .

Suy ra: MN// AC và

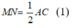
* Xét tam giác ACD có P và Q lần lượt là trung điểm của CD và AD nên PQ là đường trung bình của tam giác

Suy ra: PQ // AC và

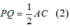
Từ (1) và (2) suy ra: MN// PQ và MN = PQ

Do đó, tứ giác MNPQ là hình bình hành.

* Ta có

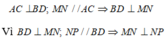
Hình bình hành MNPQ có 1 góc vuông nên là hình chữ nhật

Chọn đáp án C

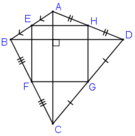
Ta có EB = EA, FB = FC (gt)

⇒ EF là đường trung bình của ΔABC

⇒EF // AC và EF = AC/2 (1)

HD = HA, GD = GC

⇒ HG là đường trung bình của ΔADC

⇒ HG // AC và HG = AC/2 (2)

Từ (1) và (2) suy ra EF // HG và EF = HG

⇒ Tứ giác EFGH là hình bình hành (*)

EA = EB, HA = HD ⇒ EH là đường trung bình của ΔABD ⇒ EH // BD.

Mà EF // AC, AC ⊥ BD

⇒ EH ⊥ EF ⇒ Ê = 90º (**)

Từ (*) và (**) suy ra EFGH là hình chữ nhật.

xét tam giác ABC có :

EA = FB (gt)

FB = FC (gt)

\(\Rightarrow EF\) là đường trung bình

\(\Rightarrow\) EF // AC và EF = \(\dfrac{1}{2}\) AC (1)

chứng minh tương tự HG là đường trung bình tam giác ADC

HG // AC và HG = \(\dfrac{1}{2}\) AC (2)

từ (1) và (2) ta suy ra EF // HG và EF = HG

\(\Rightarrow\) EFGH là hình bình hành (3)

ta có : EF // AC

EH // BD ( EH là đường trung bình tam giác ABD )

AC \(\perp\) BD ( gt )

\(\Rightarrow\) EF \(\perp\) EH

hay góc E = 90 độ (4)

từ (3) và (4) ta suy ra EFGH là hình chữ nhật

Bài giải:

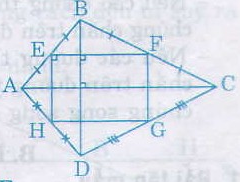
Ta có EB = EA, FB = FC (gt)

Nên EF là đường trung bình của ∆ABC

Do đó EF // AC

HD = HA, GD = GC

Nên HG là đường trung bình của ∆ADC

Do đó HG // AC

Suy ra EF // HG

Tương tự EH // FG

Do đó EFGH là hình bình hành.

EF // AC và BD ⊥ AC nên BD ⊥ EF

EH // BD và EF ⊥ BD nên EF ⊥ EH hay = 90⁰

Hình bình hành EFGH có = 90⁰ nên là hình chữ nhật.