Để chứng minh ΔMAB = ΔMAC, ta có thể sử dụng nguyên lý cắt giao. Vì AB = AC và M là trung điểm BC, nên ta có AM là đường trung trực của đoạn thẳng BC. Từ đó, ta có AM ⊥ BC. Vì AM là đường trung trực của đoạn thẳng BC, nên ta cũng có MB = MC. Như vậy, ta đã chứng minh được ΔMAB = ΔMAC.

Để chứng minh AM là tia phân giác của góc BAC, ta có thể sử dụng tính chất của tam giác cân. Vì AB = AC và AM là đường trung trực của đoạn thẳng BC, nên ta có AM là tia phân giác của góc BAC.

Để chứng minh AM ⊥ BC, ta đã chứng minh ở trên rồi. Vì AM là đường trung trực của đoạn thẳng BC, nên ta có AM ⊥ BC.

Vì AB=AC=> Tam giác ABC cân tại A

+) Tam giác ABC cân tại A có AM là tpg góc BAC

=> AM đồng thời là đường cao và đường trung tuyến

a) Do AM là đường trung tuyến 

=> M là trung điểm BC

b) Do AM là đường cao

=> AM\(\perp\)BC

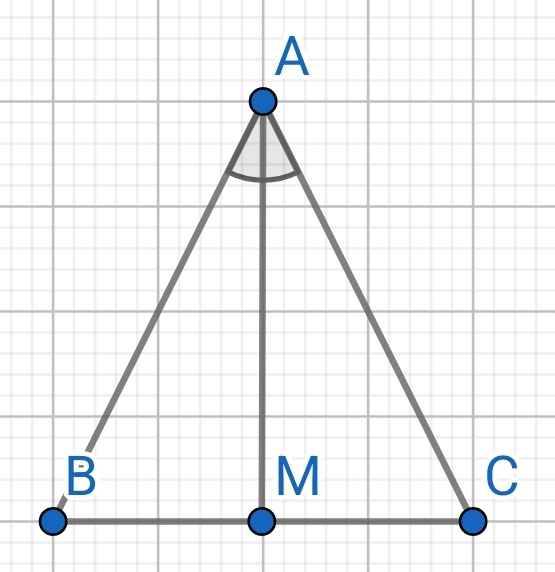 a) Do AM là tia phân giác của ∠BAC (gt)

⇒ ∠BAM = ∠CAM

Xét ∆ABM và ∆ACM có:

AM là cạnh chung

∠BAM = ∠CAM (cmt)

AB = AC (gt)

⇒ ∆ABM = ∆ACM (c-g-c)

⇒ BM = CM (hai cạnh tương ứng)

⇒ M là trung điểm của BC

b) Do ∆ABM = ∆ACM (cmt)

⇒ ∠AMB = ∠AMC (hai góc tương ứng)

Mà ∠AMB + ∠AMC = 180⁰ (kề bù)

⇒ ∠AMB = ∠AMC = 180⁰ : 2 = 90⁰

⇒ AM ⊥ BC

giúp tôi với mọi người

a) Xét \(\Delta AMC\) và \(\Delta AMB\) có:

AC = AB (gt)

CM = BM (gt,do M là trung điểm BC)

AM (cạnh chung)

     Do đó \(\Delta AMC=\Delta AMB\) (c.c.c)

\(\Rightarrow\widehat{A_1}=\widehat{A_2}\Rightarrow\) M là tia phân giác của \(\widehat{BAC}\) (1)

b) \(\Delta AMC=\Delta AMB\) (chứng minh trên)

\(\Rightarrow\widehat{M_1}=\widehat{M_2}\). Mà \(\widehat{M_1} +\widehat{M_2}=180^o\) (kề bù)

Nên \(\widehat{M_1}=\widehat{M_2}=\frac{180^o}{2}=90^o\)

Suy ra \(AM\perp BC\) (2)

Từ (1) và (2) suy ra đpcm

ai thi ioe lớp 5 vòng 11 hộ mình ko

Bài làm thì dài lắm nên mik nói qua thôi

Bài 1

a) Vì AB=AC => tam giác ABC cân tại A

=>AH là đường trung tuyến ứng với BC mà trong tam giác cân đường trung tuyến cũng chính là đường phân giác và đường trung trực nên =>đpcm

b)Vì HK=HA ;BH=CH và AH vuông góc với BC nên ABKC là hình thoi(tứ giác có 2 đường chéo cắt nhau ở trung điểm mỗi đường và vuông góc với nhau)

=>AB song song với CK (tính chất 2 cạnh đối của hình thoi)

a: Xét ΔAMB và ΔAMD có

AM chung

MB=MD

AB=AD

Do đó: ΔAMB=ΔAMD

b: Xét ΔABK và ΔADK có

AB=AD

\(\widehat{BAK}=\widehat{DAK}\)

AK chung

Do đó: ΔABK=ΔADK

c: Xét ΔKBE và ΔKDC có

KB=KD

\(\widehat{KBE}=\widehat{KDC}\)

BE=DC

Do đó: ΔKBE=ΔKDC

Suy ra: \(\widehat{BKE}=\widehat{DKC}\)

=>\(\widehat{BKE}+\widehat{BKD}=180^0\)

hay E,K,D thẳng hàng

a: Xét ΔAMB và ΔAMC có

AB=AC

AM chung

MB=MC

Do đó: ΔAMB=ΔAMC