Biết MB, MC là hai tiếp tuyến của đường tròn (O) tại B và C, góc COB=130 °. Tính số đo góc CMB.
Những câu hỏi liên quan
cho (O), lấy M nằm ngoài đường tròn. Từ M kẻ 2 tiếp tuyến MA và MB của (O). A,B là tiếp điểm. Biết cát tuyến MCD cắt (O) tại C và D (MC < MD); Góc AOC=70 độ; Góc DCB=30 độ. Tính góc AMD=?
Cho đường tròn (O; 3cm) và điểm M nằm ngoài đường tròn sao cho OM 5cm. Kẻ tiếp tuyến MB với đường tròn (O) ( B là tiếp điểm ). Từ B kẻ đường thẳng vuông góc MO tại N cắt đường tròn (O) tại C.a) CM: MC là tiếp tuyến của đường tròn (O).b) Tính độ dài MN và NO.c) Qua điểm A trên cung nhỏ BC kẻ tiếp tuyến với đường tròn (O), tiếp tuyến này cắt MB, MC lần lượt tại D và E. Tính chu vi tam giác MED.d) Tính diện tích tứ giác MBOC.
Đọc tiếp
Cho đường tròn (O; 3cm) và điểm M nằm ngoài đường tròn sao cho OM = 5cm. Kẻ tiếp tuyến MB với đường tròn (O) ( B là tiếp điểm ). Từ B kẻ đường thẳng vuông góc MO tại N cắt đường tròn (O) tại C.
a) CM: MC là tiếp tuyến của đường tròn (O).
b) Tính độ dài MN và NO.
c) Qua điểm A trên cung nhỏ BC kẻ tiếp tuyến với đường tròn (O), tiếp tuyến này cắt MB, MC lần lượt tại D và E. Tính chu vi tam giác MED.
d) Tính diện tích tứ giác MBOC.
Cho đường tròn tâm O đường kính AB và CD vuông góc với nhau . Điểm M nằm trên cung nhỏ AC sao cho
MC < MA .
a) Chứng minh CMB = DMB
b) Từ C kẻ đường vuông góc với MB cắt MD tại E và cắt AB tại F . Chứng minh tam giác MCF vuông cân .Tính số đo góc DEC
c) Chứng minh tứ giác EFDB nội tiếp được một đường tròn .Xác định tâm của đường tròn ngoại tiếp tam giác DEC
28 tháng 12 2023 lúc 8:24
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
28 tháng 12 2023 lúc 10:45
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giải chi tiết giúp mik vs nhé
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
28 tháng 12 2023 lúc 13:11
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giúp mik vs ah , mik đang cần gấppppp
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giúp mik vs ah , mik đang cần gấppppp
28 tháng 12 2023 lúc 13:36
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giúp mik vs ah , mik đang cần gấppppp
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giúp mik vs ah , mik đang cần gấppppp
b: Xét (O) có
ΔCAB nội tiếp
CB là đường kính
Do đó: ΔCAB vuông tại A
=>CA\(\perp\)AB tại A
=>CA\(\perp\)BE tại A
Ta có: \(\widehat{OAE}=\widehat{OAC}+\widehat{EAC}=\widehat{OAC}+90^0\)
\(\widehat{MAC}=\widehat{MAO}+\widehat{OAC}=\widehat{OAC}+90^0\)
Do đó: \(\widehat{OAE}=\widehat{MAC}\)
Xét tứ giác CKAE có \(\widehat{CKE}=\widehat{CAE}=90^0\)
nên CKAE là tứ giác nội tiếp
=>\(\widehat{ACK}=\widehat{AEK}\)
=>\(\widehat{ACM}=\widehat{AEO}\)
Xét ΔAMC và ΔAOE có
\(\widehat{ACM}=\widehat{AEO}\)
\(\widehat{MAC}=\widehat{OAE}\)
Do đó: ΔAMC đồng dạng với ΔAOE
=>\(\dfrac{AM}{AO}=\dfrac{AC}{AE}\)
=>\(AM\cdot AE=AO\cdot AC\)
Đúng 0
Bình luận (0)
28 tháng 12 2023 lúc 15:50
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giải chi tiết giúp mik vs nhé 1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là h...
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
28 tháng 12 2023 lúc 16:59
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.a) Cho OA 9 ,OM 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)b) Chứng minh MA . AE OA . ACc) Chứng minh EC là tiếp tuyến của (O). giải chi tiết giúp mik vs nhé
Đọc tiếp
1/ Từ điểm M ở ngoài đường tròn (O) kẻ hai tiếp tuyến MA và MB đến đường tròn O (A,B là hai tiếp điểm) MO cắt AB tại H .Kẻ đường kính BC của đường tròn (O), đường thẳng qua O vuông góc MC lần lượt cắt MC,BA tại K,E.
a) Cho OA = 9 ,OM = 15 .Tính MA và ^AMB ?(kết quả làm tròn đến phút)
b) Chứng minh MA . AE = OA . AC
c) Chứng minh EC là tiếp tuyến của (O).
giải chi tiết giúp mik vs nhé
a: Ta có: ΔOAM vuông tại A
=>\(OA^2+AM^2=OM^2\)
=>\(MA^2=15^2-9^2=144\)
=>\(MA=\sqrt{144}=12\left(cm\right)\)
Xét ΔOAM vuông tại A có \(sinAMO=\dfrac{AO}{OM}=\dfrac{3}{5}\)
nên \(\widehat{AMO}\simeq36^052'\)
Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MO là phân giác của góc AMB
=>\(\widehat{AMB}=2\cdot\widehat{AMO}\simeq73^044'\)
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB tại H
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2\)
=>\(OH\cdot OM=OC^2\)
Xét ΔOHE vuông tại H và ΔOKM vuông tại K có
\(\widehat{HOE}\) chung
Do đó: ΔOHE đồng dạng với ΔOKM
=>\(\dfrac{OH}{OK}=\dfrac{OE}{OM}\)
=>\(OK\cdot OE=OH\cdot OM\)
=>\(OK\cdot OE=OC^2\)
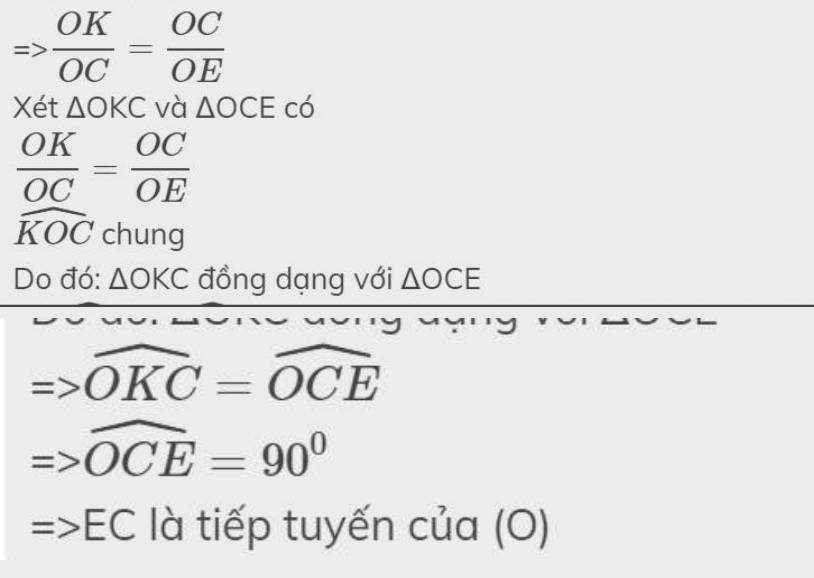
=>\(\dfrac{OK}{OC}=\dfrac{OC}{OE}\)
Xét ΔOKC và ΔOCE có
\(\dfrac{OK}{OC}=\dfrac{OC}{OE}\)
\(\widehat{KOC}\) chung
Do đó: ΔOKC đồng dạng với ΔOCE
=>\(\widehat{OKC}=\widehat{OCE}\)
=>\(\widehat{OCE}=90^0\)
=>EC là tiếp tuyến của (O)
Đúng 1
Bình luận (0)