Cho hai số x và y sao cho (4y2 -12y+25)(4x2+6x +4)=28.Tính tỉ số của y và x

Những câu hỏi liên quan
Cho hai số x và y sao cho
(4y2 -12y +25 )(4x2 +6x +4 ) = 28
thì tỉ số của y và x là
Cho 2 số x;y thỏa mãn (4y^2 - 12y + 25 )(4x^2 + 6x + 4 ) = 28 . Tính y/x
tìm cặp số thực (x,y) thỏa pt (4x^2+6x+4)(4y^2-12y+25)=28
4x2 +6x+4=7/4
4y2-12y+25>=16
=>vp >=28
dt khi
x=-3/4
y=3/2
Đúng 0
Bình luận (0)
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức
S
(
4
x
2
+
3
y
)
(
4
y
2
+
3
x
)
+
25
x
y
là: A.
M
25
2
;
m...
Đọc tiếp
Cho các số thực x; y thõa mãn x≥0; y≥0 và x+y=1. Giá trị lớn nhất M , giá trị nhỏ nhất m của biểu thức S = ( 4 x 2 + 3 y ) ( 4 y 2 + 3 x ) + 25 x y là:
A. M = 25 2 ; m = 191 16 .
B. M = 12 ; m = 191 16 .
C. M = 25 2 ; m = 12 .
D. M = 25 2 ; m = 0 .
Do x+ y= 1 nên
S = 16 x 2 y 2 + 12 ( x + y ) ( x 2 - x y + y 2 ) + 34 x y = 16 x 2 y 2 + 12 ( x + y ) 2 - 3 x y + 34 x y , d o x + y = 1 = 16 x 2 y 2 - 2 x y + 12
Đặt t= xy . Do x≥ 0 ; y≥0 nên
0 ≤ x y ≤ ( x + y ) 2 4 = 1 4 ⇒ t ∈ 0 ; 1 4
Xét hàm số f(t) = 16t2- 2t + 12 trên [0 ; 1/4].
Ta có f’ (t) = 32t- 2 ; f’(t) =0 khi t= 1/ 16 .
Bảng biến thiên
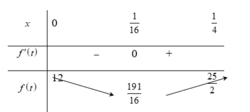
Từ bảng biến thiên ta có:
m i n 0 ; 1 4 f ( t ) = f ( 1 16 ) = 191 16 ; m a x 0 ; 1 4 f ( t ) = f ( 1 4 ) = 25 2
Vậy giá trị lớn nhất của S là 25/2 đạt được khi
x + y = 1 x y = 1 4 ⇔ x = 1 2 y = 1 2
giá trị nhỏ nhất của S là 191/ 16 đạt được khi
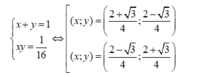
Chọn A.
Đúng 0
Bình luận (0)
tìm cặp số thực (x,y) thỏa mãn pt (4x2+6x+4)(4y2-12y+25)=28
4x2-1
X(x+y)-6x-6y
X2-2xy+y2-z2
A2+2+2a+2ab+b2-ac-bc
9x2-1 phần 4
X2-2x-4y2-4y
9(x-y)2-4(x+y)2
(3x-2y)2-(2x-3y)2
9(x-y)2-4(x+y)2
\(4x^2-1=\left(2x-1\right)\left(2x+1\right)\)
\(x\left(x+y\right)-6x-6y=\left(x+y\right)\left(x-6\right)\)
\(x^2-2xy+y^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\)
\(9x^2-\dfrac{1}{4}=\left(3x-\dfrac{1}{2}\right)\left(3x+\dfrac{1}{2}\right)\)
Đúng 0
Bình luận (0)
Cho biết x và y là hai đại lượng tỉ lệ nghịch và khi x=8 thì y = -25
a) Tìm hệ số tỉ lệ nghịch của y đối với x.
b) Hãy biểu diễn y theo x.
c) Tính giá trị của y khi x =10; x =50
\(a,\text{Gọi hstl là }a\\ \Rightarrow a=xy=8\left(-25\right)=-200\\ b,y=-\dfrac{200}{x}\\ c,x=10\Rightarrow y=-\dfrac{200}{10}=-20\\ x=50\Rightarrow y=-\dfrac{200}{50}=-4\)
Đúng 3
Bình luận (1)
Cho số hữu tỉ x=8/-15
a) Tìm hai số hữu tỉ âm y và z sao cho y+z=x
b) Tìm số hữu tỉ y bằng số hưu tỉ x sao cho tổng của tử số và mẫu số của y bằng 14
Cho số hữu tỉ x=8/15
a) Hãy tìm hai số hữu tỉ âm y và z sao cho y+z=x
b) Tìm số hữu tỉ y bằng số hữu tỉ x sao cho tổng của tử số và mẫu số của y bằng 14

















