cho tam giác ABC,các đường cao BH và CK .CMR:
a, bốn điểm B,C,H,K cùng thuộc một đường tròn
b,HK<BC
Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng :
a) Bốn điểm B, C, H, K cùng thuộc một đường tròn
b) HK < BC
Cho tam giác ABC, các đường cao BH và CK. Chứng minh: Bốn điểm B, C, H, K cùng thuộc một đường tròn
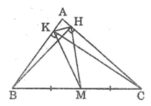
Gọi M là trung điểm của BC.
Tam giác BCH vuông tại H có HM là đường trung tuyến nên:
HM = (1/2).BC (tính chất tam giác vuông)
Tam giác BCK vuông tại K có KM là đường trung tuyến nên:
KM = (1/2).BC (tính chất tam giác vuông)
Suy ra: MB = MC = MH = MK
Vậy bốn điểm B, C, H, K cùng nằm trên một đường tròn tâm M bán kính bằng (1/2).BC.
Cho tam giác ABC các đường cao AD và BE chứng minh rằng
a) bốn điểm A, B, D, E cùng thuộc một đường tròn
b) DE<AB
a: Xét tứ giác ABDE có
\(\widehat{ADB}=\widehat{AEB}\left(=90^0\right)\)
Do đó: ABDE là tứ giác nội tiếp
hay A,B,D,E cùng thuộc một đường tròn
Cho tam giác ABC, hai đường cao BH, CK. Chứng minh:
a) 4 điểm B, K, H, C cùng thuộc 1 đường tròn
b) BK giao với CK tại I. Chứng minh 4 điểm A, H, I, K thuộc cùng 1 đường tròn
Cho tam giác ABC ( AB = AC ), vẽ các đường cao BH, CK ( H thuộc AC, K thuộc AB )
a, CMR: BH = CK
b, CMR: KH // BC
c, Tính HK biết BC = a, AB = AC = b
Cho tam giác ABC có đường cao AD và trực tâm H. Gọi I, K lần lượt là trung điểm của HA, HB. Gọi E, F lần lượt là trung điểm của BC, AC. Chứng minh:
a, Bốn điểm E, F, I, K cùng thuộc một đường tròn
b, Điểm D cũng thuộc đường tròn đi qua bốn điểm E, I, F, K
cho tam giác ABC có M là trung điểm BC. Gọi D,E theo thứ tự là chân các đường vuông góc kẻ từ M đến AB,AC. I là điểm đối xứng với B qua D, K là điểm đối xứng với C qua E, H là trung điểm IK. CMR:
a,bốn điểm B,I,K,C cùng nằm trên 1 đường tròn
b, MH vuông góc vs IK
Cho tam giác ABC vuông tại A vẽ đường thẳng a đi qua điểm A sao cho B và C thuộc cùng một nửa mặt phẳng có bờ là a .Vẽ BH, CK vuông góc với đường thẳng A HK thuộc đường thẳng A. M là trung điểm của BC.C/m:
AH = CKHK = BH+CKTam giác MHK vuông cân.a)
Xét tam giác ABH và tam giác ACK có
AHB=AHC=900
BAH=ACK ( cùng phụ với CAK)
=> tam giác ABH= tam giác ACK
=> AH=CK
b)
tam giác ABH= tam giác ACK
=> AH=CK và AK=BH
=>HK=AH+AK=BH+CK
Vậy HK=BH+CK
c)
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Các đường cao BH, CK cắt nhau tại I. M là trung điểm của AH
a) Chứng minh A, H, I, K cùng thuộc một đường tròn
b) Vẽ đường kính AD, chứng minh tam giác ACD vuông từ đó chứng minh BH // CD
c) Chứng minh tứ giác BICD là hình bình hành.
a: Xét tứ giác AHIK có
\(\widehat{AHI}+\widehat{AKI}=90^0+90^0=180^0\)
=>AHIK là tứ giác nội tiếp
=>A,H,I,K cùng thuộc một đường tròn
b: Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó ΔACD vuông tại C
=>AC\(\perp\)CD
Ta có: BH\(\perp\)AC
AC\(\perp\)CD
Do đó:BH//CD
c: Ta có: BH//CD
I\(\in\)BH
Do đó: BI//CD
Xét (O) có
ΔABD nội tiếp
AD là đường kính
Do đó; ΔABD vuông tại B
Ta có:BD\(\perp\)BA
CI\(\perp\)BA
Do đó:BD//CI
Xét tứ giác BICD có
BI//CD
BD//CI
Do đó: BICD là hình bình hành