a,tìm y: y x6+y=77 b, 6x9+6x5+6x4

Những câu hỏi liên quan
Tính giá trị của đa thức P(x)= x6-6x5+6x4-6x3+6x2-6x+1 tại x=5
\(P\left(x\right)=5^6-6.5^5+6.5^4-6.5^3+6.5^2-6.5+1=5^6-6\left(5^5-5^4-5^3-5^2-5\right)+1=1556\)
Đúng 0
Bình luận (0)
mình quên là k dùng máy tính bỏ túi nha
Đúng 0
Bình luận (0)
\(P\left(x\right)=x^6-6x^5+6x^4-6x^3+6x^2-6x+1\)
\(=x^6-5x^5-x^5+5x^4+x^4-5x^3-x^3+5x^2+x^2-5x-x+1\)
\(=x^5\left(x-5\right)-x^4\left(x-5\right)+x^3\left(x-5\right)-x^2\left(x-5\right)+x\left(x-5\right)-x+1\)
-Thay \(x=5\) vào P(x) ta được:
\(P\left(5\right)=5^5\left(5-5\right)-5^4\left(5-5\right)+5^3\left(5-5\right)-5^2\left(5-5\right)+5\left(5-5\right)-5+1\)\(=-5+1=-4\)
Đúng 1
Bình luận (0)
6x1=
6x2=
6x3=
6x4=
6x5=
6x6=
6x7=
6x8=
6x9=
6x10=
giúp mình với ai làm được mình tick cho
6x1=6
6x2=12
6x3=18
6x4=24
6x5=30
6x6=36
6x7=42
6x8=48
6x9=54
6x10=60
đúng thig k nhé
Đúng 1
Bình luận (0)
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
Đúng 0
Bình luận (0)
6x1=6
6x2=12
6x3=18
6x4=24
6x5=30
6x6=36
6x7=42
6x8=48
6x9=54
6x10=60
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bảng cửu chương 6
6x1=?
6x2=?
6x3=?
6x4=?
6x5=?
6x6=?
6x7=?
6x8=?
6x9=?
6x10=?
cố gắng nha!
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60
k mk nha
Đúng 0
Bình luận (0)
cậu trả lời rồi hỏi làm gì,nhưng đáp án đúng
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm y
y x6+y=77
\(y.6+y=77\\ y\left(6+1\right)=77\\ y.7=77\\ y=77:7\\ y=11\)
Chúc em học tốt! ![]()
Đúng 0
Bình luận (0)
y.6+y=77
y.6 + y.1 = 77
y.(6+1) =77
y.7 = 77
y = 77:7
y = 11
Vậy y bằng 11
Đúng 0
Bình luận (0)
6x5+6-6x4
6 x 5 + 6 - 6 x 4
= 30 + 6 - 6 x 4
= 30 + 6 - 24
=12
tick mình nha
Đúng 0
Bình luận (0)
6x5+6-6x4
=6x5+6x1-6x4
=6x(5+1-4)
=6x2
=12
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
6x9=
4x7=
5x2=
6x5=
4x7=
Xem thêm câu trả lời
Tìm tập xác định D của hàm số
y
3
x
−
2
+
6
x
4
−
3
x
A.
D
2
3
;
4
3...
Đọc tiếp
Tìm tập xác định D của hàm số y = 3 x − 2 + 6 x 4 − 3 x
A. D = 2 3 ; 4 3
B. D = 3 2 ; 4 3
C. D = 2 3 ; 3 4
D. D = − ∞ ; 4 3
Tìm m để phương trình
x
6
+
6
x
4
-
m
3
x
3
+
15
-
3
m
2...
Đọc tiếp
Tìm m để phương trình x 6 + 6 x 4 - m 3 x 3 + 15 - 3 m 2 x 2 - 6 m x + 10 = 0 có đúng hai nghiệm phân biệt thuộc 1 2 ; 2
A. 11 5 < m < 4
B. 2 < m ≤ 5 2
C. 0 < m < 9 4
D. 7 5 ≤ m < 3
Chọn đáp án B
Phương trình đã cho tương đương với:
![]()
![]()
![]()
Xét hàm số f t = t 3 + 3 t trên ℝ
Tacó f ' t = 3 t 2 + 3 > 0 , ∀ t ∈ ℝ nên hàm số f t đồng biến trên ℝ
Suy ra
![]()
![]()
Xét hàm số g x = x + 1 x trên 1 2 ; 2
Ta có g ' x = 1 - 1 x 2
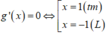
Bảng biến thiên:
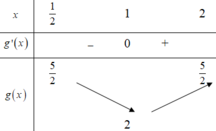
Dựa vào bảng biến thiên, để phương trình đã cho có hai nghiệm phân biệt trên 1 2 ; 2
⇔ Đường thẳng y = m cắt đồ thị hàm số g x = x + 1 x tại hai điểm phân biệt trên 1 2 ; 2
⇔ 2 < m ≤ 5 2
Đúng 0
Bình luận (0)
Tìm m để phương trình
x
6
+
6
x
4
-
m
3
x
3
+
(
15
-
3
m
2
)...
Đọc tiếp
Tìm m để phương trình x 6 + 6 x 4 - m 3 x 3 + ( 15 - 3 m 2 ) x 2 - 6 m x + 10 = 0 có đúng hai nghiệm phân biệt thuộc [1/2;2]
A. ![]()
B. ![]()
C. ![]()
D. ![]()