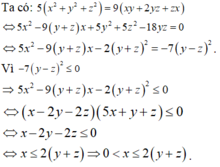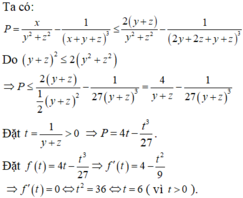\(2899=13.223\)

Vậy \(x=1,y=2,z=3\)

Có x3.2yz=2899

suy ra 200 bé hơn hoặc bằng 2yz bé hơn 300

suy ra 2899:2yz bé hơn hoặc bằng 2899:200 bé hơn 15

suy ra 2899:2yz lớn hơn 2899:300 lớn hơn 9

Có 9 bé hơn x3 và x3 bé hơn 15 nên x=1

suy ra 13 .2yz=2899

                 2yz=2899:13

                 2yz=223

suy ra y=2, z=3

                Vậy x=1,y=2,z=3

Mình làm vậy là sai ư vậy theo bạn làm thế nào mới đúng

Chọn C

Ta co : x/2=y/3;y/4=z/5

=>x/8=y/12=z/15=(x+y-z) / (8+12-15)=10/5=2

Ta có x/8=2        

=> x=16

y/12=2

=> y=24

z/15=2

=> z=30

\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2z+1\right)< 1\)

\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-1\right)^2< 1\)

Nếu tồn tại 1 trong 3 số \(x-y;y-z;z-1\) khác 0

Do x; y; z nguyên

\(\Rightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge1\) (vô lý)

\(\Rightarrow x-y=y-z=z-1=0\)

\(\Leftrightarrow x=y=z=1\)

Bài 3:

a, (\(x\)+y+z)²

=((\(x\)+y) +z)²

= (\(x\) + y)² + 2(\(x\) + y)z + z²

= \(x^2\) + 2\(xy\) + y² + 2\(xz\) + 2yz + z²

=\(x^2\) + y² + z² + 2\(xy\) + 2\(xz\) + 2yz

b, (\(x-y\))(\(x^2\) + y² + z² - \(xy\) - yz - \(xz\))

= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y³ 

Đến dây ta thấy xuất hiện \(x^3\) - y³ khác với đề bài, em xem lại đề bài nhé

c,

(\(x\) + y + z)³ 

=(\(x\) + y)³ + 3(\(x\) + y)²z + 3(\(x\)+y)z² + z³

= \(x^3\) + 3\(x^2\)y + 3\(xy^{2^{ }}\) + y³ +  3(\(x\)+y)z(\(x\) + y + z) + z³

= \(x^3\) + y³ + z³ + 3\(xy\)(\(x\) + y) + 3(\(x+y\))z(\(x+y+z\))

= \(x^3\) + y³ + z³ + 3(\(x\) + y)( \(xy\) + z\(x\) + yz + z²)

= \(x^3\) + y³ + z³ + 3(\(x\) + y){(\(xy+xz\)) + (yz + z²)}

= \(x^3\) + y³ + z³ + 3(\(x\) + y){ \(x\)( y +z) + z(y+z)}

= \(x^3\) + y³ + z³ + 3(\(x\) + y)(y+z)(\(x+z\)) (đpcm)

\(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{8}=\frac{y}{12}\)

\(\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{y}{12}=\frac{z}{15}\)

Vậy \(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)

=> x = 16; y = 24; z = 30

\(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{8}=\frac{y}{12}\) (1)

\(\frac{y}{4}=\frac{z}{5}\Rightarrow\frac{y}{12}=\frac{z}{15}\) (2)

Từ (1) và (2)

=> \(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\) và \(x+y-z=10\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)

\(\frac{x}{8}=2\Rightarrow x=8\times2=16\)

\(\frac{y}{12}=2\Rightarrow y=12\times2=24\)

\(\frac{z}{15}=2\Rightarrow z=2\times15=30\)

Ps : mình nghĩ đề là cm đẳng thức trên nhé 

Ta có : \(VT=x\left(y-z\right)-y\left(x+z\right)+z\left(x-y\right)\)

\(=xy-xz-xy-zy+xz-yz=-2yz=VP\)

vậy ta có đpcm