√-5/x²+1 có nghĩa khi nào
\(\sqrt{\dfrac{-1}{2}x+5}\) có nghĩa khi nào?
căn bậc hai của x + 5 có nghĩa khi nào
\(\sqrt{\dfrac{1+x}{x^2-1}}\) có nghĩa khi
\(\sqrt{3x-5}\) + \(\sqrt{\dfrac{2}{x-4}}\) có nghĩa khi
`\sqrt((1+x)/(x^2-1))` có nghĩa `<=> (1+x)/(x^2-1) >=0 <=> {(x>1),(-1<x<1):}`
`\sqrt(3x-5)+\sqrt(2/(x-4))` có nghĩa `<=> {(3x-5>=0),(x-4>0):} <=> x>4`
a) ĐKXĐ: \(\dfrac{1+x}{x^2-1}\ge0\)
\(\Leftrightarrow\dfrac{1}{x-1}\ge0\)
\(\Leftrightarrow x-1>0\)
hay x>1
Cho phương trình x + 1 x - 2 = x - 1 Khi x = 2 vế trái của phương trình đã cho có nghĩa không? Vế phải có nghĩa khi nào?
Khi x = 2 vế trái của phương trình đã cho không có nghĩa do mẫu bằng 0
Vế phải có nghĩ khi x - 1 ≥ 0 ⇔ x ≥ 1
√1+x + √x-2 có nghĩa khi nào 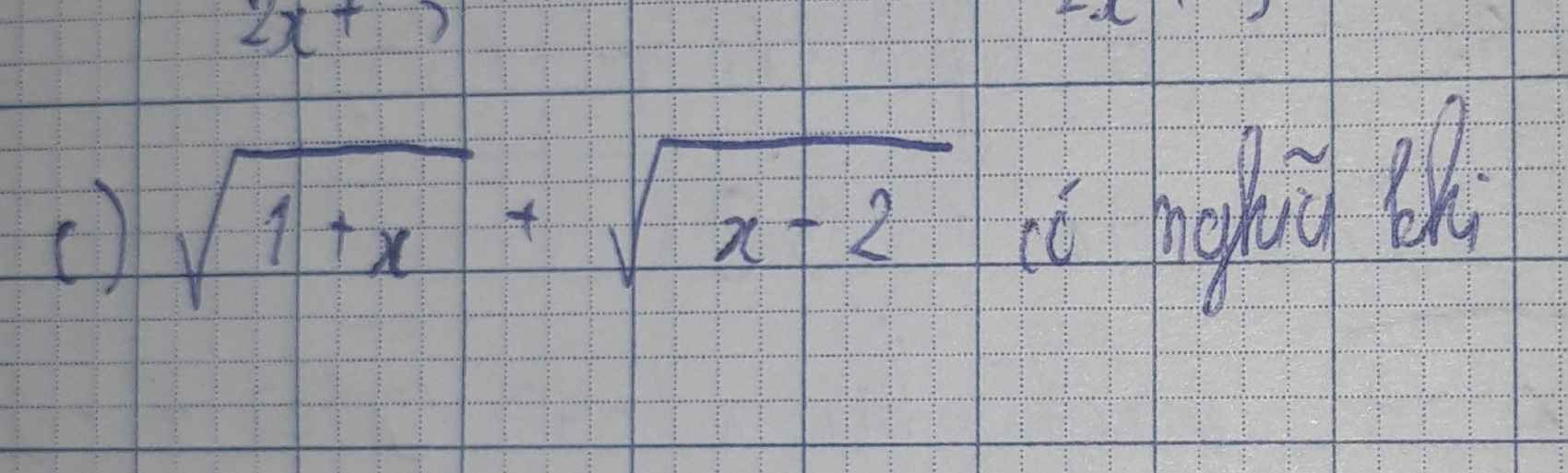
√1/-2x+5 có nghĩa khi nào
\(\sqrt{\dfrac{1}{-2x+5}}\)
\(-2x+5>0\Leftrightarrow x< \dfrac{5}{2}\)
\(\sqrt{\dfrac{1}{-2x+5}}\\ ĐK:\dfrac{1}{-2x+5}\ge0\Leftrightarrow-2x+5>0\left(-2x+5\ne0;1>0\right)\\ \Leftrightarrow x< \dfrac{5}{2}\)
\(A=\sqrt{\frac{3x-5}{x-1}}\)
a. với giá trị nào của x thì A có nghĩa
b. tìm x khi A=3
a) A có nghĩa <=> \(\frac{3x-5}{x-1}\ge0\)
<=> \(\hept{\begin{cases}3x-5\ge0\\x-1>0\end{cases}}\) hoặc \(\hept{\begin{cases}3x-5\le0\\x-1< 0\end{cases}}\)
<=> \(\hept{\begin{cases}x\ge\frac{5}{3}\\x>1\end{cases}}\)hoặc \(\hept{\begin{cases}x\le\frac{5}{3}\\x< 1\end{cases}}\)
<=> \(\orbr{\begin{cases}x\ge\frac{5}{3}\\x< 1\end{cases}}\)
b) Với \(\orbr{\begin{cases}x\ge\frac{5}{3}\\x< 1\end{cases}}\)ta có:
A = 2 <=> \(\sqrt{\frac{3x-5}{x-1}}=3\)
<=> \(\frac{3x-5}{x-1}=9\)
=> \(3x-5=9\left(x-1\right)\)
<=> \(3x-5=9x-9\)
<=> \(6x=4\)
<=> \(x=\frac{2}{3}\)(tm)
\(a,\frac{3x-5}{x-1}\ge0;x-1\ne0\)
lập TH ra đc :
\(TH1:x\ge\frac{5}{3}\)
\(TH2:x\le1;x\ne1< =>x< 1\)
vậy với \(\orbr{\begin{cases}x\ge5\\x< 1\end{cases}}\)thì A có nghĩa
\(b,A=\sqrt{\frac{3x-5}{x-1}}=3\)
\(\frac{3x-5}{x-1}=9\)
\(3x-5=9x-9\)
\(x=\frac{2}{3}\left(TM\right)\)
\(\)
Phân thức : x+2 _ x-1 xác định (hay có nghĩa) khi nào ?
\(\frac{x+2}{x-1}.\)
Điều kiện xác định: \(x-1\ne0.\)
\(\Rightarrow x\ne0+1\)
\(\Rightarrow x\ne1.\)
Vậy để phân thức \(\frac{x+2}{x-1}\) được xác định (hay có nghĩa) thì \(x\ne1.\)
Chúc bạn học tốt!
Cho biểu thức A=\(\sqrt{\frac{3x+4}{x-5}}\)và B=\(\frac{\sqrt{5x-4}}{\sqrt{x-5}}\)
a) Các biểu thức trên có nghĩa khi nào?
b)Khi nào A=B