Chọn A.

Đáp án A

Đáp án A

Đáp án A

10 điểm

Đáp án B.

Gọi khoảng cách từ một điểm bất kỳ thuộc CD đến các nguồn A, B tương ứng là d₂ và d_1­

Ta có

+ Điểm cực đại trên đoạn CD thỏa mãn:

với

Có 7 giá trị của k là  nên có 7 điểm cực đại trên CD.

+ Điểm cực tiểu trên đoạn CD thỏa mãn

,

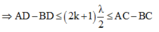
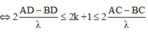
Có 6 giá trị của k thỏa mãn

 nên có 6 điểm cực tiểu trên CD.

Đáp án B

Gọi khoảng cách từ một điểm bất kỳ thuộc CD đến các nguồn A, B tương ứng là d 2 và d 1 _­

Ta có  AD − BD ≤ d 2 − d 1 ≤ AC − BC

+ Điểm cực đại trên đoạn CD thỏa mãn:  d 2 − d 1 = kλ, k = 0,  ± 1,  ± 2,  ± 3 ... với  ⇒ AD − BD ≤ kλ ≤ AC − BC ⇔ AD − BD λ ≤ k ≤ AC − BC λ

⇒ − 3 , 3 ≤ k ≤ 3 , 3

Có 7 giá trị của k là  0,  ± 1,  ± 2,  ± 3  nên có 7 điểm cực đại trên CD

+ Điểm cực tiểu trên đoạn CD thỏa mãn:  d 2 − d 1 = 2 k + 1 λ 2 , với  k = 0,  ± 1,  ± 2,  ± 3 ...

⇒ AD − BD ≤ 2 k + 1 λ 2 ≤ AC − BC ⇔ 2 AD − BD λ ≤ 2k + 1 ≤ 2 AC − BC λ ⇒ − 3 , 8 ≤ k ≤ − 2 , 83

Có 6 giá trị của k thỏa mãn  k = 0,  ± 1,  ± 2,  − 3 , − 2  nên có 6 điểm cực tiểu trên CD

\(\lambda=\frac{v}{f}=\frac{30}{15}=2cm\)

Vì 2 nguồn cùng pha nên số điểm dao động với biên độ cực đại trên đoạn AB thỏa mãn:   

\(-AB< k\lambda< AB\)    

\(\Leftrightarrow\) -8,2 < 2k < 8,2

\(k\in Z\Rightarrow k=0;^+_-1;^+_-2;^+_-3;^+_-4\)

Vậy có 9 điểm dao động với biên độ cực đại trên đoạn AB.

 Số điểm dao động với biên độ cực tiểu trên đoạn AB thỏa mãn:

       \(-AB< \left(k+0,5\right)\lambda< AB\)

 \(\Leftrightarrow\)    -8,2 < (k+0,5).2 < 8,2

 \(\Leftrightarrow\)   -4,6 < k < 3,6

     \(k\in Z\Rightarrow k=0;^+_-1;^+_-2;^+_-3;-4\)

      Vậy có 8 điểm có biên độ dao động cực tiểu trên đoạn AB.