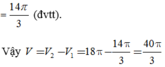các khối tròn xoay được tạo thành như thế nào?

Những câu hỏi liên quan
Câu 1: Khối đa diện được tạo thành như thế nào? Nếu đặt mặt đáy của hình hộp chữ nhật song song với mặt phẳng chiếu cạnh thì hình chiếu cạnh và hình chiếu bằng là hình gì (vẽ hình)?
Câu 2: Khối tròn xoay được tạo thành như thế nào? Nếu đặt mặt đáy của hình nón song song với mặt phẳng chiếu bằng thì hình chiếu bằng là hình gì (vẽ hình)?
Câu 1: Khối đa diện được tạo thành như thế nào? Nếu đặt mặt đáy của hình hộp chữ nhật song song với mặt phẳng chiếu cạnh thì hình chiếu cạnh và hình chiếu bằng là hình gì (vẽ hình)? (4 điểm)Câu 2: Khối tròn xoay được tạo thành như thế nào? Nếu đặt mặt đáy của hình nón song song với mặt phẳng chiếu bằng thì hình chiếu bằng là hình gì (vẽ hình)? (3 điểm)Câu 3: Hãy vẽ hình chiếu đứng, hình chiếu bằng và hình chiếu cạnh của vật thể ở hình dưới đây (3điểm)
Đọc tiếp
Câu 1: Khối đa diện được tạo thành như thế nào? Nếu đặt mặt đáy của hình hộp chữ nhật song song với mặt phẳng chiếu cạnh thì hình chiếu cạnh và hình chiếu bằng là hình gì (vẽ hình)? (4 điểm)
Câu 2: Khối tròn xoay được tạo thành như thế nào? Nếu đặt mặt đáy của hình nón song song với mặt phẳng chiếu bằng thì hình chiếu bằng là hình gì (vẽ hình)? (3 điểm)
Câu 3: Hãy vẽ hình chiếu đứng, hình chiếu bằng và hình chiếu cạnh của vật thể ở hình dưới đây (3điểm)
Khối tròn xoay được tạo thành như thế nào? Nếu đặt mặt của hình nón song song với mặt phẳng chiều cạnh thì hình chiếu đứng, chiếu bằng và chiếu cạnh có hình dạng gì ?
Khối tròn xoay được tạo thành khi nào? Các hình chiếu có đặc điểm gì?
- Khối tròn xoay được tạo thành khi quay một hình phẳng quanh một trục cố định (trục quay) của hình.
- Đặc điểm hình chiếu của khối tròn xoay:
+Khối tròn xoay thường được biểu diễn bằng hình chiếu đứng và hình chiếu bằng
Đặc điểm là: mỗi hình chiếu thể hiện được 2 trong 3 kích thước: chiều dài, chiều rộng, chiều cao
Đúng 0
Bình luận (0)
Để tạo thành các khối tròn xoay : hình trụ, hình nón, hình cầu .Ta làm thế nào khi vẽ hình chiếu của một vật thể có khối tròn xoay ta chỉ cần biểu diễn mấy hình chiếu . Vì sao ?
Mọi người giúp mình với nha
Cho hình phẳng trong hình bên (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo thành được tính theo công thức nào trong các công thức sau đây? A.
V
π
∫
a
b
g
2
x
-
f
2
x
dx
B....
Đọc tiếp
Cho hình phẳng trong hình bên (phần tô đậm) quay quanh trục hoành. Thể tích khối tròn xoay tạo thành được tính theo công thức nào trong các công thức sau đây?
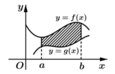
A. V = π ∫ a b g 2 x - f 2 x dx
B. V = π ∫ a b f 2 x - g 2 x dx
C. V = π ∫ a b f x - g x 2 dx
D. V = π ∫ a b f x - g x dx
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn
O
2
. Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo...
Đọc tiếp
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
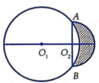
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Cho hai đường tròn
O
1
;
5
và
O
2
;
5
cắt nhau tại 2 điểm A,B sao cho AB là 1 đường kính của đường tròn
O
2
.
Gọi (D) là hình phẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần tô màu...
Đọc tiếp
Cho hai đường tròn O 1 ; 5 và O 2 ; 5 cắt nhau tại 2 điểm A,B sao cho AB là 1 đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi 2 đường tròn (ở ngoài đường tròn lớn, phần tô màu như hình vẽ). Quay (D) quanh trục O 1 ; O 2 ta được 1 khối tròn xoay. Tính thể tích khối tròn xoay được tạo thành.
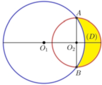
A. V = 36 π .
B. V = 68 π 3 .
C. V = 14 π 3 .
D. V = 40 π 3 .
Đáp án D.
Gắn hệ trục tọa độ Oxy sao cho O 1 ≡ O (gốc tọa độ).
Phương trình đường tròn O 1 ; 5 là x 2 + y 2 = 5 2 ⇒ y = ± 25 − x 2 .
Tam giác O 1 O 2 A vuông tại O 2 , có O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4.
Phương trình đường tròn O 2 ; 3 là x − 4 2 + y 2 = 9 ⇒ y = ± 9 − x − 4 2 .
Gọi V 1 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 1 được giới hạn bởi các đường y = 9 − x − 4 2 , y = 0 , x = 4 , x = 7 quanh trục tung ⇒ V 1 = π ∫ 4 7 9 − x − 4 2 d x .
Gọi V 2 là thể tích của khối tròn xoay sinh ra khi quay hình phẳng D 2 được giới hạn bởi các đường y = 25 − x 2 , y = 0 , x = 4 , x = 5 quanh trục tung ⇒ V 2 = π ∫ 4 5 25 − x 2 d x .
Khi đó, thể tích cần tính là:
V = V 1 − V 2 = π ∫ 4 7 9 − x − 4 2 d x − π ∫ 4 5 25 − x 2 d x = 40 π 3 .
Đúng 0
Bình luận (0)
Cho hai đường tròn
O
1
;
5
và
O
2
;
3
cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn
O
2
. Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn...
Đọc tiếp
Cho hai đường tròn O 1 ; 5 và O 2 ; 3 cắt nhau tại hai điểm A, B sao cho AB là một đường kính của đường tròn O 2 . Gọi (D) là hình phẳng được giới hạn bởi hai đường tròn (ở ngoài đường tròn lớn, phần gạch chéo như hình vẽ). Quay (D) quanh trục O 1 O 2 ta được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành
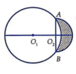
A. V = 14 π 3
B. V = 68 π 3
C. V = 40 π 3
D. V = 36 π
Đáp án C

Chọn hệ tọa độ Oxy như hình vẽ với O 3 ≡ O , O 2 C ≡ O x , O 2 A ≡ O y .
Ta có
O 1 O 2 = O 1 A 2 − O 2 A 2 = 5 2 − 3 2 = 4 ⇒ O 1 − 4 ; 0 .
Phương trình đường tròn O 1 : x + 4 2 + y 2 = 25.
Phương trình đường tròn O 2 : x 2 + y 2 = 9.
Kí hiệu H 1 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x = 0 khi x ≥ 0 .
Kí hiệu H 2 là hình phẳng giới hạn bởi các đường O 2 : x 2 + y 2 = 9, trục Oy: x=0 khi x ≥ 0 .
Khi đó thể tích V cần tìm chíình bằng thể tích V 2 của khối tròn xoay thu được khi quay hình H 2 xung quanh trục Ox (thể tích nửa khối cầu bán kính bằng 3) trừ đi thể tích V 1 của khối tròn xoay thu được khi quay hình H 1 xung quanh trục Ox.
Ta có V 2 = 1 2 . 4 3 π 3 3 = 18 π (đvtt);
V 1 = π ∫ 0 1 y 2 d x = π ∫ 0 1 25 − x + 4 2 d x = 14 π 3 (đvtt).
Vậy V = V 2 − V 1 = 18 π − 14 π 3 = 40 π 3 (đvtt).
Đúng 0
Bình luận (0)