đưa cho mik cái sách vs

chờ mik tí nha bn

Mk lia mất quyển sách lớp 4 zùi

3,4 - x + 1,7 = 1,05

        x + 1,7 = 3,4 - 1,05

        x + 1,7 = 2,35

                x = 2,35 - 1,7

                x = 0,65

3,4-x+1,7=1,05

x+1,7=3,4-1,05

x+1,7=2,35

x=2,35-1,7

x=0,65

3,4-x+1,7=1,05

3,4 + 1.7 - 1.05 = x

x = 4.05

4:

a: A=1/3(1+1/2+...+1/64)

Đặt B=1+1/2+...+1/64

=>2B=2+1+...+1/32

=>B=2-1/64=127/64

=>A=1/3*127/64=127/192

b: =5/2(1-1/3+1/3-1/5+...+1/11-1/13)

=5/2*12/13

=60/26=30/13

chữ xấu dữ vậy

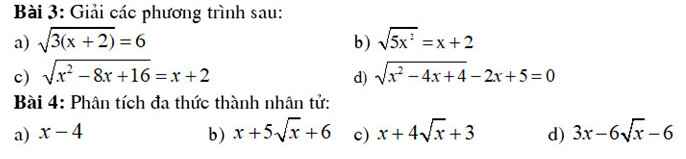
Bài 4: 

a: \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)

b: \(x+5\sqrt{x}+6=\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\)

c: \(x+4\sqrt{x}+3=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)

d: \(3x-6\sqrt{x}-6=3\left(x-\sqrt{x}-2\right)=3\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)

Bài 3:

a) \(\sqrt{3\left(x+2\right)}=6\left(đk:x\ge-2\right)\)

\(\Leftrightarrow3\left(x+2\right)=36\)

\(\Leftrightarrow3x=30\Leftrightarrow x=10\)(thỏa đk)

b) \(\sqrt{5x^2}=x+2\left(đk:x\ge-2\right)\)

\(\Leftrightarrow5x^2=\left(x+2\right)^2\)

\(\Leftrightarrow4x^2-4x-4=0\)

\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2=\dfrac{5}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{\sqrt{5}}{2}\\x-\dfrac{1}{2}=-\dfrac{\sqrt{5}}{2}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt{5}}{2}\\x=\dfrac{1-\sqrt{5}}{2}\end{matrix}\right.\)(thỏa đk)

c) \(\sqrt{x^2-8x+16}=x+2\left(1\right)\left(đk:x\ge-2\right)\)

\(\Leftrightarrow\sqrt{\left(x-4\right)^2}=x+2\Leftrightarrow\left|x-4\right|=x+2\)

TH1: \(x\ge4\)

\(\left(1\right)\Leftrightarrow x-4=x+2\Leftrightarrow-4=2\)(vô lý)

TH2: \(-2\le x< 4\)

\(\left(1\right)\Leftrightarrow4-x=x+2\)

\(\Leftrightarrow x=1\)(thỏa đk)

d) \(\sqrt{x^2-4x+4}-2x+5=0\left(đk:x\ge\dfrac{5}{2}\right)\)

\(\Leftrightarrow\sqrt{\left(x-2\right)^2}-2x+5=0\left(2\right)\Leftrightarrow\left|x-2\right|-2x+5=0\)

TH1: \(x\ge2\)

\(\left(2\right)\Leftrightarrow x-2-2x+5=0\)

\(\Leftrightarrow x=3\)(thỏa đk)

TH2: \(\dfrac{5}{2}\le x< 2\)

\(\left(2\right)\Leftrightarrow2-x-2x+5=0\)

\(\Leftrightarrow x=\dfrac{7}{3}\)(không thỏa đk)

Bài 4:

a) \(x-4=\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)\)

b) \(x+5\sqrt{x}+6=\left(\sqrt{x}+\dfrac{5}{2}\right)^2-\dfrac{1}{4}=\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)\)

c) \(x+4\sqrt{x}+3=\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)

d) \(3x-6\sqrt{x}-6=3\left(\sqrt{x}-1-\sqrt{3}\right)\left(\sqrt{x}-1+\sqrt{3}\right)\)

Bài 3:

a: Ta có: \(\sqrt{3\left(x+2\right)}=6\)

\(\Leftrightarrow3\left(x+2\right)=36\)

\(\Leftrightarrow x+2=12\)

hay x=10

b: Ta có: \(\sqrt{5x^2}=x+2\)

\(\Leftrightarrow5x^2=x^2-4x+4\)

\(\Leftrightarrow4x^2+4x-4=0\)

\(\Leftrightarrow x^2+x-1=0\)

\(\text{Δ}=1^2-4\cdot1\cdot\left(-1\right)=5\)

Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{-1-\sqrt{5}}{2}\left(nhận\right)\\x_2=\dfrac{-1+\sqrt{5}}{2}\left(nhận\right)\end{matrix}\right.\)

c: Ta có: \(\sqrt{x^2-8x+16}=x+2\)

\(\Leftrightarrow\left|x-4\right|=x+2\)

\(\Leftrightarrow4-x=x+2\left(x< 4\right)\)

\(\Leftrightarrow-2x=-2\)

hay x=1(nhận)

Bài đâu bn?

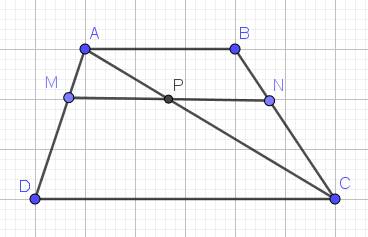
Bài 4:

Quãng đường bạn An đi: $BD$

Quãng đường bạn Hải đi: $CD$
Do $AB\parallel NC$ nên áp dụng định lý Talet, tỉ số quãng đường bạn An đi so với bạn Hải đi là:
$\frac{BD}{CD}=\frac{AB}{NC}=\frac{AB}{AM}=\frac{1}{2}$
Vậy bạn An đi quãng đường bằng 1/2 quãng đường Hải đi

Mà vận tốc 2 bạn như nhau nên thời gian An đi bằng 1/2 thời gian Hải đi

Bạn An đến D lúc 8h, xuất phát từ 7h30 nên thời gian An đi là: 8h-7h30'=30'=0,5h

Thời gian Hải đi để đến gặp An lúc 8h là: $0,5.2=1$ (h)

Vậy Hải phải xuất phát lúc: $8h-1h=7h$

Bài 3:

a. Xét tam giác $ADC$ có $MP\parallel DC$ nên áp dụng định lý Talet:

$\frac{AM}{MD}=\frac{AP}{PC}(1)$

Xét tam giác $ACB$ có $PN\parallel AB$ nên áp dụng định lý Talet:

$\frac{AP}{PC}=\frac{BN}{NC}(2)$

Từ $(1); (2)\Rightarrow \frac{AM}{MD}=\frac{BN}{NC}$

b.

Áp dụng định lý Talet với tam giác $ADC$, $MP\parallel DC$:

$\frac{MP}{DC}=\frac{AM}{AD}=\frac{AM}{AM+MD}=\frac{AM}{AM+2AM}=\frac{1}{3}$

$\Rightarrow MP=DC:3=6:3=2$ (cm)

Theo kết quả phần a:

$\frac{BN}{NC}=\frac{AM}{MD}=\frac{AM}{2AM}=\frac{1}{2}$
$\Rightarrow NC=2BN$

Áp dụng định lý Talet cho tam giác $ACB$, có $PN\parallel AB$:

$\frac{PN}{AB}=\frac{CN}{CB}=\frac{CN}{CN+BN}=\frac{2BN}{2BN+BN}=\frac{2}{3}$

$\Rightarrow PN=\frac{2}{3}AB=\frac{2}{3}.4=\frac{8}{3}$ (cm)

$MN=MP+PN=2+\frac{8}{3}=\frac{14}{3}$ (cm)

Hình vẽ:

3:Gọi chiều dài, chiều rộng là a,b

Chu vi là 64 nên a+b=64/2=32

Theo đề, ta có hệ:

a+b=32 và (a-2)(b+3)=ab+30

=>a+b=32 và 3a-2b=36

=>a=20 và b=12

1,2 + 2,3 + 3,4 - 4,5 + 5,6 - 6,7 + 7,8 - 8,9 + 9,1 = 9,3

bạn phúc làm sai rồi phải bằng 5,5 cơ

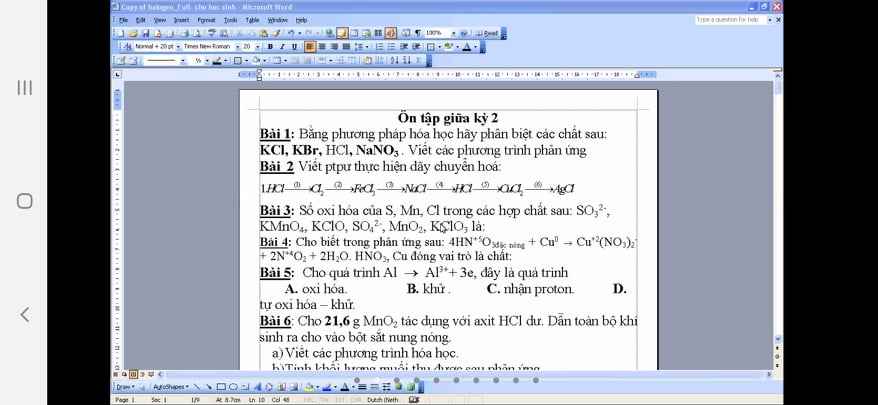
Ôn tập để thi tốt thì bạn nên tự làm nhé

Chứ bạn hỏi thì bài ôn ra chẳng để lm j