cho 2 hình bình hành ABCD và AB'C'D' chung đỉnh A. chứng minh:
BB' →+ DD'→= CC'→
Những câu hỏi liên quan
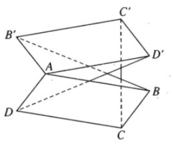
Trong không gian cho hai hình bình hành ABCD và AB'C'D' chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ \(\overrightarrow{BB'},\overrightarrow{CC'},\overrightarrow{DD'}\) đồng phẳng ?
Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ
B
B
→
,
C
C
→
,
D
D
→
đồng phẳng.
Đọc tiếp
Trong không gian cho hai hình bình hành ABCD và A’B’C’D’ chỉ có chung nhau một điểm A. Chứng minh rằng các vectơ B B ' → , C C ' → , D D ' → đồng phẳng.
Ta có: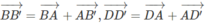 
Do đó: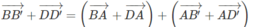 
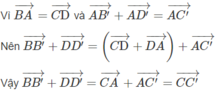
Hệ thức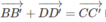 
biểu thị sự đồng phẳng của ba vectơ B B ' → , C C ' → , D D ' →
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Qua đường thẳng d không có điểm chung với hình bình hành. Gọi AA', BB', CC', DD' lần lượt là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng d. Chứng minh rằng: AA' + CC' = BB' + DD' .
(hình bạn tự vẽ nha)CM:gọi giao điểm của hai đường chéo là Omà tứ giác ABCD là hình bình hành(gt)=>\(OA=OC=\frac{1}{2}ACvàOD=OB=\frac{1}{2}BD\)kẻ OO' vuông góc với dta có:OO',AA',BB',CC',DD' vuông góc với d nên OO',AA',BB',CC',DD' song song với nhau
cm OO' là đường trung bình của hình thang BB'D'D=>\(OO'=\frac{BB'+DD'}{2}\left(1\right)\)
chứng minh OO' là đường trung bình của hình thang AA'C'C=>\(OO'=\frac{AA'+CC'}{2}\left(2\right)\)từ (1) và (2)=>\(\frac{AA'+CC'}{2}=\frac{BB'+DD'}{2}\Rightarrow AA'+CC'=BB'+D'D\)
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD và đường thẳng d nằm ngoài hình bình hành. Gọi A',B',C',D' theo thứ tự là hình chiếu của các đỉnh A,B,C,D lên đường thẳng d
Chứng minh: AA'+CC'=BB'+DD'
Cho hình bình hành ABCD. Qua C kẻ đường thẳng xy chỉ có 1 điểm chung C với hình bình hành. Gọi AA', BB', CC', DD' là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Chứng minh rằng: AA' = BB' + DD'.
Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA’; BB’; CC’, DD’ là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA', BB', CC', DD'
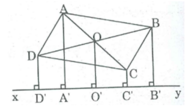
Gọi O là giao điểm của AC và BD
⇒ OA = OC, OB = OD (tính chất hình bình hành)
Kẻ OO' ⊥ xy
AA' ⊥ xy (gt)
CC' ⊥ xy (gt)
Suy ra: AA' // OO' // CC'
Tứ giác ACC'A' là hình thang có:
OA = OC (chứng minh trên)
OO' // AA' nên OO' là đường trung bình của hình thang ACC'A'.
⇒ OO' = (AA' + CC') / 2 (t/chất đường trung bình của hình thang) (1)
BB' ⊥ xy
DD' ⊥ xy (gt)
OO' ⊥ xy (gt)
Suy ra: BB'// OO' // DD'
Tứ giác BDD'B' là hình thang có:
OB = OD (Chứng minh trên)
OO' // BB' nên OO' là đường trung bình của hình thang BDD'B'.
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung bình của hình thang) (2)
Từ (1) và (2) => AA' + CC' = BB + DD'
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi AA', BB' CC', DD' là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy. Tìm mối liên hệ độ dài giữa AA', BB', CC', DD' ?
cho hình bình hành ABCD. Gọi d là đường thẳng qua A và cắt đoạn thẳng BD. Gọi BB', CC', DD' lần lượt là khoảng cách từ B, C, D đến đường thẳng d. Chứng minh rằng |BB'-DD'|=CC'
Cho hình bình hành ABCD. Ở miền trong hình bình hành ABCD vẽ hình bình hành A'B'C'D'. Gọi M,N,P,Q lần lượt là trung điểm AA', BB', CC', DD'. chứng minh MNPQ là hình bình hành?
Cho hình bình hành ABCD và đường thẳng d nằm ngoài hình bình hành . Gọi A' ,B' ,C' , D' theo thứ tự là hình chiếu của các đỉnh A,B,C,D trên đường thẳng d
C/Minh : AA" + CC'=BB' = DD'