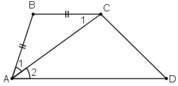
* Để chứng minh ABCD là hình thang ta cần chứng minh AD // BC.

Thông thường để chứng minh hai đường thẳng song song ta có thể chọn một trong các cách:

+ Chứng minh hai góc so le trong bằng nhau hoặc hai góc đồng vị bằng nhau.

+ Chứng minh hai đường thẳng cùng song song hoặc cùng vuông góc với đường thẳng thứ ba.

Ở bài này ta sẽ đi chứng minh hai góc so le trong bằng nhau là góc A2 và C1.

Theo giả thiết ta có:

Mà hai góc này ở vị trí so le trong

⇒ AD // BC

Vậy ABCD là hình thang (đpcm).

Vì \(\Delta ABC\) cân tại B ( vì AB =BC) 

=> Góc BAC = góc BCA (1) 

Vì AC là phân giác góc A 

=> góc BAC = góc CAD (2) 

Từ (1) và (2) => góc BCA = góc CAD 

Mà 2 góc này ở vị trí so le trong

=> AD // BC 

=>  ABCD là hình thang

Vậy ________________

Bài giải:

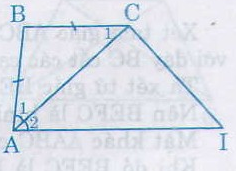
Ta có AB = BC (gt)

Suy ra ∆ABC cân

Nên $\widehat{A_1}=\widehat{C_1}$ (1)

Lại có $\widehat{A_1}=\widehat{A_2}$ (2) (vì AC là tia phân giác của $\hat{A}$)

Từ (1) và (2) suy ra $\widehat{C_1}=\widehat{A_2}$

nên BC // AD (do $\widehat{C_1},\widehat{A_2}$ ở vị trí so le trong)

Vậy ABCD là hình thang

Ta có AB = BC (gt)

Suy ra: ∆ABC cân.

Nên \(\widehat{A_1}=\widehat{C_1}\) (1)

Lại có (2) (vì AC là tia phân giác của )

Từ (1) và (2) suy ra

nên BC // AD (do ở vị trí so le trong)

Vậy ABCD là hình thang.