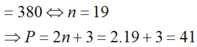tìm giá trị n nguyên dương : a) 1/8.16n=2n

Những câu hỏi liên quan
Tìm số nguyên dương lớn nhất sao cho n2+2n+1 / n+23 có giá trị nguyên
Cho A=\(\frac{n+1}{2n-1}\)(n thuộc Z)
Tìm n để A có giá trị là 1 số nguyên dương
Để A nguyên dương
=> n + 1 \(⋮\)2n - 1
Tiếp theo dễ rồi nhé :)
Đúng 0
Bình luận (0)
Để A thuộc N* <=> n+1/2n-1 thuộc N*
Xét 2A= 2n+2/2n-1
Ta cm 2n+2/2n-1 thuộc N*
<=> 2n-1+3/2n-1 thuộc N*
<=> 1+ 3/ 2n-1 thuộc N*
<=> 2n-1 thuộc Ư(3)
Ư(3) = { 1 -1 3 -3 }
=> 2n-1 thuộc {1 -1 3 - 3 }
Sau đó tìm n rồi xét xem với gtri nào của n thì A lớn hơn 0 là xog r đó bạn
Đúng 0
Bình luận (0)
Để \(\frac{n+1}{2n-1}\) là 1 số nguyên số
\(\Rightarrow n+1⋮2n-1\)
\(\Rightarrow2\left(n-1\right)+3⋮2n-1\)
\(\Rightarrow3⋮2n-1\)
\(\Rightarrow2n-1\inƯ\left(3\right)\) Mà n là 1 số nguyên dương
\(\Rightarrow2n-1\in\left\{1;3\right\}\)
\(\Rightarrow2n\in\left\{2;4\right\}\)
\(\Rightarrow n\in\left\{1;2\right\}\)
Đúng 0
Bình luận (0)
tìm giá trị nguyên dương của x để 6x2-11x+6 chia hết cho 2x-3
tìm giá trị nguyên của x để x2+2x-6 chia hết cho x+4
tìm số nguyên n để giá trị của 2n2+3n+3 chia hết cho giá trị của 2n-1
Giúp mình mấy bài này nha
bài 1 : Tìm n thuộc N để phân số 2n-1/3n+2 có giá trị là số nguyên dương
Bài 2: Tìm n thuộc N để phân số n+3/4n-1 có giá trị là số nguyên âm
Bài 3: Tìm n thuộc N để phân số 2n+5/3n+1 có giá trị là số tự nhiên
tìm số nguyên dương n lớn nhất sao cho n2+2n+1 phần n+23 có giá trị nguyên
Muốn \(\frac{n^2+2n+1}{n+23}\) có giá trị nguyên thì:
\(n^2+2n+1⋮n+23\Rightarrow n^2+2n+1-n.\left(n+23\right)⋮n+23\)
\(\Rightarrow n^2+2n+1-n^2-23n⋮n+23\)
\(\Rightarrow-21n+1⋮n+23\Rightarrow-21n+1+21\left(n+23\right)⋮n+23\)
\(\Rightarrow-21n+1+21n+23⋮n+23\)
\(\Rightarrow24⋮n+23\Rightarrow n+23\inƯ\left(24\right)\)
Mà n lớn nhất nên: n+23 lớn nhất => n+23 = 24 => n=1
Vậy n = 1
Đúng 0
Bình luận (0)
Cho mình xin lỗi:
\(-21n+1⋮n+23\Rightarrow-21n+1+21\left(n+23\right)⋮n+23\)
\(\Rightarrow-21n+1+21n+483⋮n+23\Rightarrow484⋮n+23\)
Mà n là số nguyên dương lớn nhất nên: n+23=484 => n = 461
Vậy n = 461
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho A = n3+3n2+2n. Tìm giá trị nguyên dương của n với n<10 để A chia hết cho 15
cho \(A=\frac{2n+9}{n+1}\)
a,tìm n để A là phân số
b,tìm n để A là số nguyên
c,tìm n để A nhận giá trị âm
đ,tìm n để A nhận giá trị dương
a) Gọi d là ước nguyên tố của 2n+9/n+1. Ta có:
2n+9-2(n+1) chia hết cho d => d=7
Ta thấy 2n+9 chia hết cho 7 khi đó n+1 chia hết cho 7.
<=> 2n+9-7 chia hết cho 7.
<=>2(n+1) chia hết cho 7 <=> n+1 chia hết cho 7 <=> n=7k-1(k thuộc N)
Vậy nếu n khác 7k-1 thì A là phân số.
Đúng 0
Bình luận (0)
tìm các giá trị nguyên của n để giá trị của biểu thức \(A=\dfrac{2n^2+3n+3}{2n-1}\) có giá trị là số nguyên
Để A là số nguyên thì 2n^2-n+4n-2+5 chia hết cho 2n-1
=>\(2n-1\in\left\{1;-1;5;-5\right\}\)
=>\(n\in\left\{1;0;3;-2\right\}\)
Đúng 0
Bình luận (0)
`2n^2+3n+3 | 2n-1`
`-` `2n^2-n` `n+2`
------------------
`4n+3`
`-` `4n-2`
------------
`5`
`<=> (2n^2+3n+3) : (2n-1)=5`
`<=> 5 ⋮ (2n-1)=> 2n-1 ∈ Ư(5)`\(=\left\{1,5\right\}\)
`+, 2n-1=1=>2n=2=>n=1`
`+, 2n-1=-1=>2n=0=>n=0`
`+, 2n-1=5=>2n=6=>n=3`
`+,2n-1=-5=>2n=-4=>n=-2`
vậy \(n\in\left\{1;0;3;-2\right\}\)
Đúng 0
Bình luận (0)
Gọi n là số nguyên dương sao cho
1
log
3
x
×
1
log
3
3
x
+
1
log
3
2...
Đọc tiếp
Gọi n là số nguyên dương sao cho 1 log 3 x × 1 log 3 3 x + 1 log 3 2 x + . . . . . + 1 log 3 n x = 190 log 3 x đúng với mọi x dương, x ≠ 1 . Tìm giá trị của biểu thức P = 2 n + 3
A. P = 23.
B. P = 41.
C. P = 43.
D. P = 32.
tìm số nguyên dương n lớn nhất sao cho \(\frac{n^2+2n+1}{n+23}\) có giá trị nguyên