abc+acd=bca

Những câu hỏi liên quan
tìm a,b,c,d thuộc N biết abc + acd = bca
Cho tam giác ABC vuông tại B có AC=8cm góc BCA=54°.trên nữa mặt phẳng bờ AC không chứa điểm B dựng tam giác ABC có AD=9,6cm góc ACD=74°.tính số đo góc ACD
Cho tam giác nhọn ABC có góc C = 40 độ. Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD
a) Chứng minh rằng tam giác AKH đồng dạng với tam giác BCA
b) Tính số đo góc AKH
a) - Ta có: SABCD=AH.BC=AK.AB.
=>\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\)
- Ta có: \(\widehat{ABC}+\widehat{BAD}=180^0\) (AD//BC).
=>\(\widehat{ABC}+\widehat{BAH}+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(90^0+\widehat{HAK}+\widehat{KAD}=180^0\)
=>\(\widehat{HAK}+\widehat{KAD}=90^0\) mà \(\widehat{KAD}+\widehat{ADK}=90^0\) (tam giác ADK vuông tại K) nên \(\widehat{HAK}=\widehat{ADK}\) mà \(\widehat{ADK}=\widehat{ABC}\) (ABCD là hình bình hành) nên\(\widehat{HAK}=\widehat{ABC}\)
- Xét tam giác AKH và tam giác BCA có:
\(\dfrac{AH}{AK}=\dfrac{AB}{BC}\) (cmt)
\(\widehat{HAK}=\widehat{ABC}\) (cmt)
=> Tam giác AKH ∼ Tam giác BCA (c-g-c).
b) - Ta có: Tam giác AKH ∼ Tam giác BCA (cmt) nên:
\(\widehat{AKH}=\widehat{ACB}=40^0\) (2 góc tương ứng)
Đúng 1
Bình luận (0)
cho tam giác abc vuông tại a có b=60. tia phân giác của góc abc cắt ac tại m. mh vuông bc. cd vuông bm. a, cm ab=bh. b, cm góc bca= góc acd. c, ab và cd cắt nhau tại S. tính độ dài ab biết am =1cm
hình dễ nên tự vẽ
a, xét 2 t.giác vuông ABM và HBM có:
BM cạnh chung
\(\widehat{ABM}\)=\(\widehat{HBM}\)(gt)
=> t.giác ABM=t.giác HBM(cạnh huyền- góc nhọn)
=> AB=BH(2 cạnh tương ứng)
b, ta có: \(\widehat{ABM}\)+\(\widehat{BAM}\)+\(\widehat{AMB}\)=180 độ
=>30 độ+90 độ +\(\widehat{AMB}\)=180 độ
=>\(\widehat{AMB}\)=60 độ mà \(\widehat{AMB}\)=\(\widehat{CMD}\)(vì đối đỉnh)
=>\(\widehat{CMD}\)=60 độ
xét t.giác MCD có: \(\widehat{CMD}\)+\(\widehat{MDC}\)+\(\widehat{MCD}\)=180 độ
=>60 độ+ 90 độ+ \(\widehat{MCD}\)=180 độ
=>\(\widehat{MCD}\)=30 độ(1)
Mặt khác \(\Delta\)ABC có:\(\widehat{ABC}\)+\(\widehat{BAC}\)+\(\widehat{ACB}\)=180 độ
=>60 độ+90 độ+\(\widehat{ACB}\)=180 độ
=> \(\widehat{ACB}\)=30 độ(2)
từ (1) và (2) suy ra\(\widehat{BCA}\)=\(\widehat{ACD}\)
c,
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn có C =40 . Vẽ hbh ABCD , Gọi AH , AK theo thứ tự là đường cao của các tia p/g của ABC , ACD .
a, CM : tam giác AKH đồng dạng với tam giác BCA
b,tính góc AKH = ???
Cho tam giác ABC nhọn (AC < AB) nội tiếp đường tròn O đường kính AD. Đường cao CF và BG cắt nhau tại H kẻ OI vuông BC
a) Chứng minh tứ giác CFBD nội tiếp đường tròn
b)chứng minh tam giác ACD đồng dạng tam giác CFB
c)chứng minh tứ giác CHBD là hình bình hành và CD.CG=BD.BF
d)chứng minh I, H, D thẳng hàng
Cứu với ạ
Trong hình tam giác ABC cân tại A. Gọi M là trung điểm của BC
a) c/m tam giác ABM bằng tam giác ACM
b) Trên tia đối của tia MA lấy điểm D sao cho MA = MD. c/m AB song song CD
c) tam giác acd là tam giác gì? Vì sao?
\(\text{#TNam}\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB=AC,` \(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABM` và Tam giác `ACM:`
`AB=AC (CMT)`
\(\widehat{B}=\widehat{C}\)
`MB=MC (g``t)`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`b,` Xét Tam giác `AMB` và Tam giác `CMD:`
`AM=MD (g``t)`
\(\widehat{AMB}=\widehat{CMD}\) `( \text {2 góc đối đỉnh})`
`MB = MC (g``t)`
`=> \text {Tam giác AMB = Tam giác CMD (c-g-c)}`
`->`\(\widehat{ABC}=\widehat{DCB}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong
`-> \text {AB // CD}`
`c,` Vì Tam giác `AMB =` Tam giác `CMD (b)`
`-> AB=CD (\text {2 cạnh tương ứng})`
Mà `AB = AC (a)`
`-> AC = CD`
Xét Tam giác `ACD: AC = CD`
`-> \text {Tam giác ACD cân tại C}`
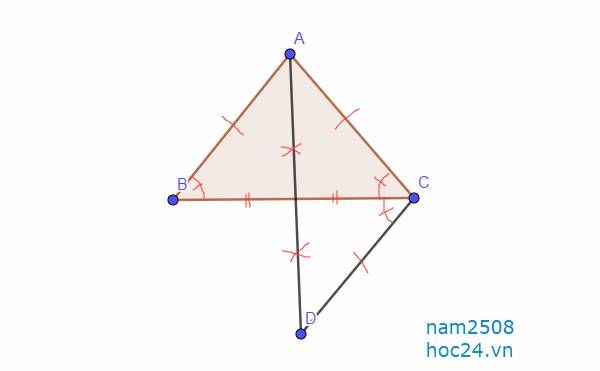
Đúng 0
Bình luận (0)
Bài 7: Cho tam giác ABC vuông tại A. Gọi M là trung điểm của BC; trên tia đối của tia MA lấy điểm D sao cho MA=MD.
a) Chứng minh: Tam giác AMB = tam giác DMC ; AB = DC ; AB//DC ; ^ACD = 90 độ
b) Chứng minh: tam giác BCA = tam giác DAC ; BC = AD
c) Chứng minh: AM = 1/2 BC
AM BC
a: Xét ΔAMB và ΔDMC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔAMB=ΔDMC
Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AB//DC và AB=DC; \(\widehat{ACD}=90^0\)
b:
Ta có: ABDC là hình chữ nhật
nên AD=BC
XétΔBCA và ΔDAC có
BC=DA
CA chung
BA=DC
Do đó: ΔBCA=ΔDAC
Đúng 0
Bình luận (1)
a: Xét ΔAMB và ΔDMC có
MA=MD
MB=MC
Do đó: ΔAMB=ΔDMC
Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà
nên ABDC là hình chữ nhật
Suy ra: AB//DC và AB=DC;
b:
Ta có: ABDC là hình chữ nhật
nên AD=BC
XétΔBCA và ΔDAC có
BC=DA
CA chung
BA=DC
Do đó: ΔBCA=ΔDAC
Đúng 0
Bình luận (1)
Cho tam giác ABC vuông tại a ,trên nửa mặt phẳng bờ BC (không chứa A ),kẻ tia Bx sao cho xBC=BCA
a)Chứng tỏ AC//Bx
b)Chứng minh AB vuông góc với Bx
c )Trên tia Bx lấy điểm D sao cho góc ACD =120 dộ.Tính góc CDB,góc CDx?
help meeee!

























