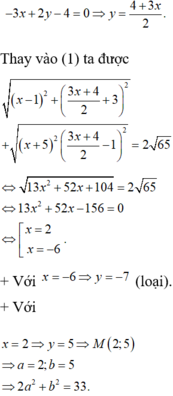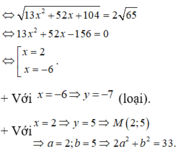Cho hai số dương a,b thỏa mãn \(\frac{a}{5}\)\(=\frac{b}{6}\)và 2a2-b2=56. Khi đó a+b=...........

Những câu hỏi liên quan
Cho 2 số dương a,b thỏa mãn : \(\frac{a}{5}\)= \(\frac{b}{6}\) và 2a^2 - b^2 =56 .Khi đó a+b = ...
\(\frac{a}{5}=\frac{b}{6}\Rightarrow\frac{a^2}{25}=\frac{b^2}{36}=\frac{2a^2-b^2}{50-36}=\frac{56}{14}=4\)
\(\Rightarrow\) a2 = 100; b2 = 144
\(\Rightarrow\) a = 10; b = 12 (vì a,b > 0)
\(\Rightarrow\) a + b = 10 + 12 = 22
Đúng 0
Bình luận (0)
cho hai số dương a;b thỏa mãn a/5=b/6 biết2a^2-b^2=56 khi đó a+b= ?
cho 2 số dương a b thỏa mãn: a/5=b/6 và 2a^2-b^2=56 khi đó a+b=
Cho số phức z thỏa mãn
z
-
1
+
3
i
+
z
¯
+
5
+
i
2
65
Giá trị nhỏ nhất của
z
+
2
+
i...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
![]()
![]()
![]()
![]()
Cho hai số dương a;b thõa mãn : a/5= b/6 và 2a^2 -b^2=56. Khi đó a+b= ?
\(\frac{a}{5}=\frac{b}{6}=>\frac{a^2}{25}=\frac{b^2}{36}=>\frac{2a^2}{50}=\frac{b^2}{36}\)
áp dụng .... ta có;
\(\frac{2a^2}{50}=\frac{b^2}{36}=\frac{2a^2-b^2}{50-36}=\frac{56}{14}=4\)
từ 2a^2/50=4=>2a^2=200=>a^2=100=>a=+10
b^2/36=4=>b^2=144=>b=+12
vì a;b là 2 số dương >a=10;b=12
khi đó a+b=10+12=22
tick đúng cho tớ nhé
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn |z - 1 + 3i|+|z + 5 + i| 2
65
Giá trị nhỏ nhất của |z + 2 + i| đạt được khi z a + bi với a,b là các số thực dương. Giá trị của
2
a
2
+
b
2
bằng A. 17 B. 33 C. 24 D. 36
Đọc tiếp
Cho số phức z thỏa mãn
|z - 1 + 3i|+|z + 5 + i| = 2 65 Giá trị nhỏ nhất của
|z + 2 + i| đạt được khi z = a + bi với a,b là các số thực dương. Giá trị của 2 a 2 + b 2 bằng
A. 17
B. 33
C. 24
D. 36
cho 2 số dương a,b thỏa mãn : \(\frac{a}{5}\)=\(\frac{b}{6}\)va 2a2 - b2 =56 khi do a+b= ?
\(\frac{a}{5}=\frac{b}{6}=>\frac{a^2}{25}=\frac{b^2}{36}=>\frac{2a^2}{50}=\frac{b^2}{36}\)
áp dụng ... ta có:
\(\frac{2a^2}{50}=\frac{b^2}{36}=\frac{2a^2-b^2}{50-36}=\frac{56}{14}=4\)
=>a^2/25=4=>a^2=100=>a=10
=>b^2/36=4=>b^2=144=>b=12
=>a+b=10+12=22
Đúng 0
Bình luận (0)
cho 3 số thực dương không âm thỏa mãn a+b+c1
tìm MAX của P√a2+2b2+√b2+2c2+√c2+2a2
Đọc tiếp
cho 3 số thực dương không âm thỏa mãn a+b+c=1
tìm MAX của
Dấu "=" xảy ra khi và các hoán vị
Đúng 2
Bình luận (0)
cho hai số dương a;b thỏa mản: a/5=b/6 và 2a^2-b^2= 56 khi đó a+b bằng bao nhiêu