a.

\(x^3-7x+6=0\)

\(\Leftrightarrow x^3-3x^2+2x+3x^2-9x+6=0\)

\(\Leftrightarrow x\left(x^2-3x+2\right)+3\left(x^2-3x+2\right)=0\)

\(\Leftrightarrow\left(x^2-3x+2\right)\left(x+3\right)=0\)

\(\Leftrightarrow\left(x^2-x-2x+2\right)\left(x+3\right)=0\)

\(\Leftrightarrow\left[x\left(x-1\right)-2\left(x-1\right)\right]\left(x+3\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+3\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-3\end{matrix}\right.\)

f.

\(x^4-4x^3+12x-9=0\)

\(\Leftrightarrow x^4-4x^3+3x^2-3x^2+12x-9=0\)

\(\Leftrightarrow x^2\left(x^2-4x+3\right)-3\left(x^2-4x+3\right)=0\)

\(\Leftrightarrow\left(x^2-4x+3\right)\left(x^2-3\right)=0\)

\(\Leftrightarrow\left(x^2-x-3x+3\right)\left(x^2-3\right)=0\)

\(\Leftrightarrow\left[x\left(x-1\right)-3\left(x-1\right)\right]\left(x^2-3\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x^2-3\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=1\\x=3\\x=\pm\sqrt{3}\end{matrix}\right.\)

g.

\(x^5-5x^3+4x=0\)

\(\Leftrightarrow x\left(x^4-5x^2+4\right)=0\)

\(\Leftrightarrow x\left(x^4-x^2-4x^2+4\right)=0\)

\(\Leftrightarrow x\left[x^2\left(x^2-1\right)-4\left(x^2-1\right)\right]=0\)

\(\Leftrightarrow x\left(x^2-1\right)\left(x^2-4\right)=0\)

\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)\left(x-2\right)\left(x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x=\pm1\\x=\pm2\end{matrix}\right.\)

1) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x+5y=50\\10x-6y=6\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}11y=44\\2x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)

Vậy hpt có nghiệm (x;y) = (3;4)

2)

a) 3x² - 2x - 1 = 0

\(\Leftrightarrow3x^2-3x+x-1=0\)

\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)

\(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)

Vậy pt có nghiệm x = 1 hoặc x = 3

b) Đặt x² = t (t \(\ge\) 0)

Pt trở thành: t² - 20t + 4 = 0

\(\Delta\) = (-20)² - 4.1.4 = 400 - 16 = 384

=> pt có 2 nghiệm phân biệt t₁ = \(\dfrac{20+8\sqrt{6}}{2}=10+4\sqrt{6}\)

t₂ = \(\dfrac{20-8\sqrt{6}}{2}=10-4\sqrt{6}\)

=> x₁ = \(\sqrt{10+4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}=2+\sqrt{6}\)

x₂ = \(2-\sqrt{6}\)

Cả ba phương trình trên đều là phương trình trùng phương.

a)  3 x 4   –   12 x 2   +   9   =   0   ( 1 )

Đặt x 2   =   t ,  t ≥ 0.

(1) trở thành:  3 t 2   –   12 t   +   9   =   0   ( 2 )

Giải (2):

Có a = 3; b = -12; c = 9

⇒ a + b + c = 0

⇒ (2) có hai nghiệm  t 1   =   1   v à   t 2   =   3 .

Cả hai nghiệm đều thỏa mãn điều kiện.

+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1

Vậy phương trình có tập nghiệm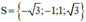 

b)  2 x 4   +   3 x 2   –   2   =   0   ( 1 )

Đặt x 2   =   t , t ≥ 0.

(1) trở thành:    2 t 2   +   3 t   –   2   =   0   ( 2 )

Giải (2) :

Có a = 2 ; b = 3 ; c = -2

⇒   Δ   =   3 2   –   4 . 2 . ( - 2 )   =   25   >   0

⇒ (2) có hai nghiệm

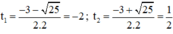
t 1   =   - 2   <   0  nên loại.

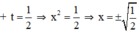
Vậy phương trình có tập nghiệm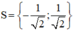 

c)  x 4   +   5 x 2   +   1   =   0   ( 1 )

Đặt  x 2   =   t ,   t   >   0 .

(1) trở thành:  t 2   +   5 t   +   1   =   0   ( 2 )

Giải (2):

Có a = 1; b = 5; c = 1

⇒   Δ   =   5 2   –   4 . 1 . 1   =   21   >   0

⇒ Phương trình có hai nghiệm:

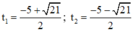
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.

Vậy phương trình (1) vô nghiệm.

( 36x +12x5 - 8x4 + 10x3 - 6x2 + 2x - 1) : (x4 + 4x3 - 3x2 + 2x - 1)

=12x-56

Dư 120x³-98x²+112x+55

(Mình tính ra nháp r hí hí)

- Ta có:

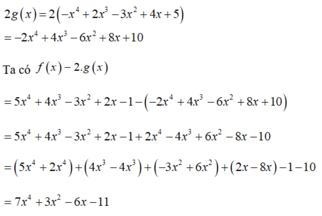
Hệ số cần tìm là -11

Chọn đáp án C

+) Ta có

2 g ( x ) = 2 − x 4 + 2 x 3 − 3 x 2 + 4 x + 5 = − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10  Ta có  f ( x ) − 2 ⋅ g ( x ) = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 − − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10 = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 + 2 x 4 − 4 x 3 + 6 x 2 − 8 x − 10 = 5 x 4 + 2 x 4 + 4 x 3 − 4 x 3 + − 3 x 2 + 6 x 2 + ( 2 x − 8 x ) − 1 − 1 = 7 x 4 + 3 x 2 − 6 x − 11

Hệ số cần tìm là -11

Chọn đáp án C

Chọn D.

Ta có: f’(x) = -4x³ + 12x² – 6x + 2.

Nên f’(-1) = 24.

a)  x 4   –   5 x 2   +   4   =   0   ( 1 )

Đặt x 2   =   t, điều kiện t ≥ 0.

Khi đó (1) trở thành :  t 2   –   5 t   +   4   =   0   ( 2 )

Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm  t 1   =   1 ;   t 2   =   c / a   =   4

Cả hai giá trị đều thỏa mãn điều kiện.

+ Với t = 1 ⇒ x 2   =   1  ⇒ x = 1 hoặc x = -1;

+ Với t = 4 ⇒ x 2   =   4  ⇒ x = 2 hoặc x = -2.

Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.

b)  2 x 4   –   3 x 2   –   2   =   0 ;   ( 1 )

Đặt   x 2   =   t , điều kiện t ≥ 0.

Khi đó (1) trở thành :  2 t 2   –   3 t   –   2   =   0   ( 2 )

Giải (2) : Có a = 2 ; b = -3 ; c = -2

⇒   Δ   =   ( - 3 ) 2   -   4 . 2 . ( - 2 )   =   25   >   0

⇒ Phương trình có hai nghiệm

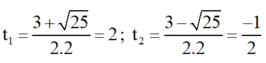
Chỉ có giá trị t 1   =   2  thỏa mãn điều kiện.

+ Với t = 2 ⇒ x 2   =   2  ⇒ x = √2 hoặc x = -√2;

Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.

c)  3 x 4   +   10 x 2   +   3   =   0   ( 1 )

Đặt x 2   =   t , điều kiện t ≥ 0.

Khi đó (1) trở thành :  3 t 2   +   10 t   +   3   =   0   ( 2 )

Giải (2) : Có a = 3; b' = 5; c = 3

⇒  Δ ’   =   5 2   –   3 . 3   =   16   >   0

⇒ Phương trình có hai nghiệm phân biệt

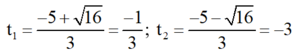
Cả hai giá trị đều không thỏa mãn điều kiện.

Vậy phương trình (1) vô nghiệm.

a) Đa thức thương 4x – 11 và đa thức dư 26x – 10.

b) Đa thức thương 2 x 2  – 3x + 5 và đa thức dư 3x + 4.