Chứng minh rằng M nằm trong đường tròn đường kính AB <=> góc AMB > 90o

Những câu hỏi liên quan
Chứng minh rằng M nằm ngoài đường tròn đường kính AB <=> góc AMB < 90o
(=>) Gọi C là giao của AM và đtr
tam giác ABC nội tiếp đtr đường kính AB => tam giác ABC vuông tại C => góc ACB = 900 => góc MCB = 90o
=> Tam giác MCB vuông tại C => góc CMB < 90o Hay góc AMB < 90o
(<=) Giả sử M nằm trong đtr
Gọi C là giao của AM và đtr
Tam giác ACB vuông tại C => góc ACB = 90o
Mà góc AMB là góc ngoài của tam giác MCB tại M => góc AMB > góc MCB = 90o => Mâu thuẫn với đề bài
Vậy điều giả sử sai => M nằm ngoài đtr
Vậy...
Đúng 1
Bình luận (0)
Cho đường tròn tâm O bán kính 5cm điểm M nằm ngoài đường tròn kẻ các tiếp tuyến MA,MB với đường tròn ,biết góc AMB=60° a, chứng minh MA=MB b, chứng minh ∆AMB là ∆ đều
a: Xét (O) có
MA,MB là tiếp tuyến
nên MA=MB
b: Xét ΔMAB có MA=MB và góc AMB=60 độ
nên ΔMAB đều
Đúng 0
Bình luận (0)
Cho (O), dây cung AB không trùng với đường kính. Lấy một điểm M bất kỳ thuộc đường tròn AB. Chứng minh rằng góc AMB = 1/2 góc AOB
Cho đường tròn o , điểm M nằm ngoài đường tròn . kẻ các tiếp tuyến MA,MB với đường tròn (B,C là các tiếp điểm) a,Chứng minh ∆AMB cân b,Cho góc AMB=60°.Tính gócAOB c,Chứng minh MO vuông góc AB
a: Xét (O) có
MA,MB là tiếp tuyến
Do đó: MA=MB
=>ΔMAB cân tại M
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AMB}+\widehat{AOB}=360^0\)
=>\(\widehat{AOB}+60^0+90^0+90^0=360^0\)
=>\(\widehat{AOB}+240^0=360^0\)
=>\(\widehat{AOB}=120^0\)
c: ta có: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
=>MO\(\perp\)AB
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng: ∠COD 90o
Đọc tiếp
Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
∠COD = 90o
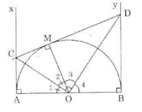
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của ∠AOM
OD và tia phân giác của ∠BOM
OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.
=> ∠COD = 90o (đpcm)
Đúng 2
Bình luận (0)
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB 60 độa: Chứng minh AMB là tam giác đềub: Tính chu vi tam giác AMBc: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xya: tứ giác APMQ là hình gì? Vì sao?b: gọi I là trung điểm PQ. Chứn...
Đọc tiếp
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB= 60 độ
a: Chứng minh AMB là tam giác đều
b: Tính chu vi tam giác AMB
c: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?
Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xy
a: tứ giác APMQ là hình gì? Vì sao?
b: gọi I là trung điểm PQ. Chứng minh OI vuông góc AM
Bài 1:
a: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay ΔMAB cân tại M
mà \(\widehat{AMB}=60^0\)
nên ΔMBA đều
b: Xét ΔAOM vuông tại A có
\(AM=OA\cdot\tan30^0\)
nên \(AM=5\sqrt{3}\left(cm\right)\)
\(C_{AMB}=3\cdot AM=15\sqrt{3}\left(cm\right)\)
c: Ta có: MA=MB
nên M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của AB
hay MO⊥AB(1)
Xét (O) có
ΔABC nội tiếp
AC là đường kính
DO đó: ΔABC vuông tại B
Suy ra: AB⊥BC(2)
Từ (1) và (2) suy ra OM//BC
hay BMOC là hình thang
Đúng 0
Bình luận (0)
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB 60 độa: Chứng minh AMB là tam giác đềub: Tính chu vi tam giác AMBc: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xya: tứ giác APMQ là hình gì? Vì sao?b: gọi I là trung điểm PQ. Chứng minh OI...
Đọc tiếp
Bài1 : Cho đường tròn (O,5cm) điểm M nằm bên ngoài đường tròn. Kể các tiếp tuyến MA, MB với đường tròn ( AB là tiếp điểm) biết góc AMB= 60 độ
a: Chứng minh AMB là tam giác đều
b: Tính chu vi tam giác AMB
c: Tia AO cắt đường tròn ở C; tứ giác BMOC là hình gì? Vì sao?
Bài 2 : Cho đường tròn (O) đường kính AB, gọi M là một điểm tùy ý trên đường tròn, xy là tiếp tuyến của đường tròn tại A, qua M kẻ MP vuông góc AB, MQ vuông góc xy
a: tứ giác APMQ là hình gì? Vì sao?
b: gọi I là trung điểm PQ. Chứng minh OI vuông góc AM
c
Gọi H là giao điểm của AB và OM
a, Xét Δv MAO và ΔvMBO
Có MO chung
AO=OB(=bk)
=> ΔvMAO= ΔMBO (ch-cgv)
=> MA=MB
Trong ΔAMB
Có MA=MB(cmt)
=> ΔAMB cân tại M
lại có góc AMB=60 độ
=> ΔAMB là Δ đều
b, Ta có: góc AMO=góc BMO ( ΔvMAO= ΔvMBO)
mà góc AMO+ góc BMO= góc AMB=60 độ
=> góc AMO=\(\frac{1}{2}.60=30^0\)
Áp dụng tỉ số lượng giác
Ta có : tan góc AMO=\(\frac{AO}{AM}\)
tan30=\(\frac{5}{AM}\)
=>AM=\(\frac{5}{tan30}=5\sqrt{3}\)
Chu vi ΔAMB= AM.3=\(5\sqrt{3}.3=15\sqrt{3}\)
c, Ta có OA=OB (=bk)
=> O thuộc đường trung trực AB(1)
MA=MB(cmt)
=> M thuộc đường trung trực AB (2)
Từ (1)(2)=> OM là cả đường trung trực
=> MO vuông góc AB (*)
Ta có: OA=OB=OC(=bk)
=> OB=\(\frac{1}{2}AC\)
mà OB là đường trung tuyến
=> Δ ABC vuông tại B
=> AB vuông góc BC(**)
Từ (*)(**)=> MO//BC
=> BMOC là hình thang
Đúng 0
Bình luận (1)
Bài 2:
a,
Ta có : góc AQM=90 độ ( MQ vuông góc xy)
góc APM =90 độ ( MP vuông góc AB)
góc QAP=90độ ( xy vuông góc OA)
=> QMPA là hình chữ nhật
b, Trong hình chữ nhật QMPA:
Có : I là trung điểm của đường chéo thứ nhất QP
-> I cũng là trung điểm của đường chéo thứ 2 AM
=> IA=IM
=> OI vuông góc AM tại I ( đường kính đi qua trung điểm => vuông góc ( đ/Lý 3)
Đúng 0
Bình luận (1)
Cho đường tròn tâm O đường kính AB. Một tiếp tuyến của đường tròn tại P cắt đường thẳng AB tại T (điểm B nằm giữa O và T). Chứng minh:
B T P ^ + 2 . T P B ^ = 90 o
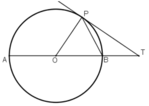
Cách 1:
+  là góc tạo bởi tiếp tuyến PT và dây PB
là góc tạo bởi tiếp tuyến PT và dây PB

+ PT là tiếp tuyến của đường tròn (O)
⇒ PT ⊥ OP
⇒ ΔOPT vuông tại P
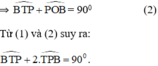
Cách 2:
ΔPBT có: 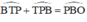 (định lý góc ngoài tam giác) (1)
(định lý góc ngoài tam giác) (1)
ΔOPB có OP = OB (= R)
⇒ ΔOPB cân tại O
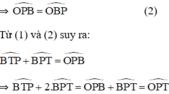
PT là tiếp tuyến của đường tròn (O)
⇒ PT ⊥ OP
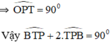
Đúng 0
Bình luận (0)
cho đường tròn o đường kính ab . vẽ đường tròn tâm a cắt đường tròn o tại c và d. kẻ dây bn của đường tròn cắt (a) tại e nằm trong đường tròn. chứng minh rằng góc cen=góc edn, ne2=nc.nd
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
=>CB\(\perp\)CA tại C
=>CB là tiếp tuyến của (A;AC)
Xét (A;AC) có
\(\widehat{BCE}\) là góc tạo bởi tiếp tuyến CB và dây cung CE)
\(\widehat{CDE}\) là góc nội tiếp chắn cung CE
Do đó: \(\widehat{BCE}=\widehat{CDE}\)
Xét (O) có
\(\widehat{CBE}\) là góc nội tiếp chắn cung CN
\(\widehat{CDN}\) là góc nội tiếp chắn cung CN
Do đó: \(\widehat{CBE}=\widehat{CDN}\)
mà \(\widehat{BCE}=\widehat{CDE}\)
nên \(\widehat{CBE}+\widehat{BCE}=\widehat{CDN}+\widehat{CDE}=\widehat{NDE}\left(1\right)\)
Xét ΔCEB có \(\widehat{CEN}\) là góc ngoài tại đỉnh E
nên \(\widehat{CEN}=\widehat{CBE}+\widehat{BCE}\left(2\right)\)
Từ(1) và (2) suy ra \(\widehat{CEN}=\widehat{NDE}\)
AC=AD
=>A nằm trên đường trung trực của CD(3)
OC=OD
=>O nằm trên đường trung trực của CD(4)
Từ (3) và (4) suy ra OA là đường trung trực của CD
=>BA là đường trung trực của CD
=>\(sđ\stackrel\frown{BC}=sđ\stackrel\frown{BD}\)
Xét (O) có
\(\widehat{BNC}\) là góc nội tiếp chắn cung BC
\(\widehat{BND}\) là góc nội tiếp chắn cung BD
\(sđ\stackrel\frown{BC}=sđ\stackrel\frown{BD}\)
Do đó: \(\widehat{BNC}=\widehat{BND}\)
Xét ΔCEN và ΔEDN có
\(\widehat{CEN}=\widehat{EDN}\)
\(\widehat{CNE}=\widehat{END}\)
Do đó: ΔCEN đồng dạng với ΔEDN
=>\(\dfrac{NC}{NE}=\dfrac{NE}{ND}\)
=>\(NE^2=NC\cdot ND\)
Đúng 0
Bình luận (0)












